
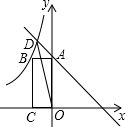
 如图,在平面直角坐标系xOy中,直线y=-x+3交y轴于点A,交反比例函数y=$\frac{k}{x}$(k<0)的图象于点D,y=$\frac{k}{x}$(k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD.
如图,在平面直角坐标系xOy中,直线y=-x+3交y轴于点A,交反比例函数y=$\frac{k}{x}$(k<0)的图象于点D,y=$\frac{k}{x}$(k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD.分析 (1)根据矩形的面积求出AB,求出反比例函数的解析式;
(2)解方程组求出反比例函数与一次函数的交点,确定点D的坐标,根据三角形的面积公式计算即可.
解答 解:(1)∵矩形OABC的面积为4,双曲线在第二象限,
∴k=-4,
∴反比例函数的表达式为y=-$\frac{4}{x}$;
(2))∵直线y=-x+3交y轴于点A,
∴点A的坐标为(0,3),即OA=3,
解方程组$\left\{\begin{array}{l}{y=-x+3}\\{y=-\frac{4}{x}}\end{array}\right.$,
得$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=4}\end{array}\right.$,
∵点D在第二象限,
∴点D的坐标为(-1,4),
∴△AOD的面积=$\frac{1}{2}$×3×1=$\frac{3}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握反比例函数的系数k的几何意义、解方程组求出反比例函数与一次函数的交点是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
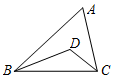 如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
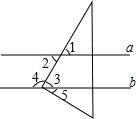 如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )
如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )| A. | ∠1=50° | B. | ∠2=50° | C. | ∠4=130° | D. | ∠5=30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a-2a=a | B. | $\sqrt{2}+\sqrt{5}$=$\sqrt{7}$ | C. | (2a)3=2a3 | D. | a6÷a3=a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 班级 节次 | 1班 |
| 第1节 | 语文 |
| 第2节 | 英语 |
| 第3节 | 数学 |
| 第4节 | 音乐 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数(名) | 2 | 4 | 3 | 1 |
| A. | 12 | B. | 13 | C. | 13.5 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com