
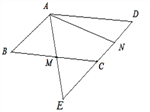
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
【答案】![]()
【解析】分析:延长DC和AM交于E,过点E作EH⊥AN于点H,易证△ABM≌△ECM,再证得AB=![]() NE,因为AN=2,AE=2AM=2,且∠MAN=60°,可得∠AEH=30°,AH=
NE,因为AN=2,AE=2AM=2,且∠MAN=60°,可得∠AEH=30°,AH=![]() AE=1,根据勾股定理可得EH =
AE=1,根据勾股定理可得EH =![]() ,EN=2,即可得AB=
,EN=2,即可得AB=![]() .
.
详解:
如图,延长DC和AM交于E,过点E作EH⊥AN于点H.
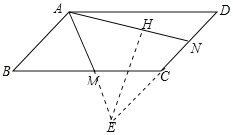
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,
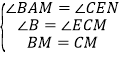 ,
,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=![]() AB,即AB=
AB,即AB=![]() NE,
NE,
∵AN=2,AE=2AM=2,且∠MAN=60°,
∴∠AEH=30°,
∴AH=![]() AE=1,
AE=1,
∴EH=![]() =
=![]() ,
,
∴NH=AN-AH=2-1=1,
∴EN=![]() =2,
=2,
∴AB=![]() ×2=
×2=![]() ;
;
故答案为:![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
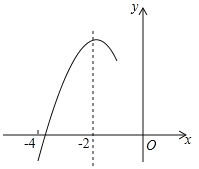
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() )是该抛物线上的点,则
)是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
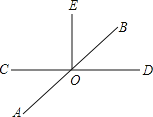
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() ,
,![]() ,
,![]() ,
,![]() 为原点,点
为原点,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() .且
.且![]() 、
、![]() 满足
满足![]() .
.
(1)填空:![]() ;
;![]() .
.
(2)点![]() 把线段
把线段![]() 分成两条线段,其中一条是另一条线段的3倍,则
分成两条线段,其中一条是另一条线段的3倍,则![]() 的值为: .
的值为: .
(3)着![]() 为2,动点
为2,动点![]() 从点
从点![]() 出发,以每秒2个单位长度速度沿数轴负方向运动,同时,动点
出发,以每秒2个单位长度速度沿数轴负方向运动,同时,动点![]() 从点
从点![]() 出发,以每秒3个单位长度速度沿数轴正方向运动,求运动多少秒时点
出发,以每秒3个单位长度速度沿数轴正方向运动,求运动多少秒时点![]() 把线段
把线段![]() 分成两条线段且其中一条是另一条线段的3倍?
分成两条线段且其中一条是另一条线段的3倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是正方形网格中的三个格点.
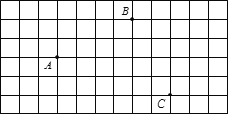
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
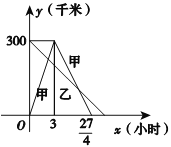
【题目】已知:甲乙两车分别从相距300千米的A,B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,它们在行驶过程中何时相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止.

(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;
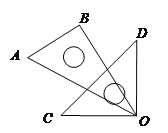
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?
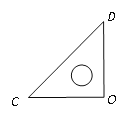

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个加工厂计划为某开发公司加工一批产品,已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且单独加工这批产品甲厂比乙厂要多用20天,已知由甲厂单独做,公司需付甲厂每天费用180元;若由乙厂单独做,公司需付乙厂每天费用220元.
(1)求加工的这批产品共有多少件?
(2)若由一个加工厂单独加工完成,选用哪个加工厂费用较低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
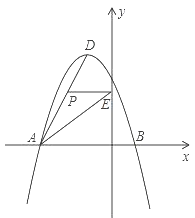
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com