
分析 先找出分子、分母的公因式,再约分即可.
解答 解:$\frac{{-14{a^2}b{c^3}}}{{21{a^3}bc}}$=$\frac{7{a}^{2}bc•(-2{c}^{2})}{7{a}^{2}bc•3a}$=-$\frac{2{c}^{2}}{3a}$,
$\frac{{{x^2}-9}}{{{x^2}-6x+9}}$=$\frac{(x+3)(x-3)}{(x-3)^{2}}$=$\frac{x+3}{x-3}$.
故答案为-$\frac{2{c}^{2}}{3a}$,$\frac{x+3}{x-3}$.
点评 本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.约分的关键是找出分子、分母的公因式.确定公因式要分为系数、字母、字母的指数来分别确定.注意:①分式约分的结果可能是最简分式,也可能是整式.②当分子与分母含有负号时,一般把负号提到分式本身的前面.③约分时,分子与分母都必须是乘积式,如果是多项式的,必须先分解因式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | .甲 大于乙 | B. | .甲小于乙 | C. | .甲等于乙 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
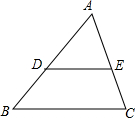 如图,点D、E分别在△ABC的边AB、AC上,下列条件不能使△ADE∽△ABC相似的是( )
如图,点D、E分别在△ABC的边AB、AC上,下列条件不能使△ADE∽△ABC相似的是( )| A. | DE∥BC | B. | AD:AB=DE:BC | C. | AD:DB=AE:EC | D. | ∠BDE+∠DBC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴,y轴分别交于A、B两点,以AB为边在第一象限内作矩形ABCD,使AD=5
如图,在直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴,y轴分别交于A、B两点,以AB为边在第一象限内作矩形ABCD,使AD=5查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com