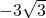
分析:作AC⊥x轴与C,BD⊥x轴于D,AE⊥BD于E点,设A点坐标为(3a,-

a),则OC=-3a,AC=-

a,利用勾股定理计算出OA=-2

a,得到∠AOC=30°,再根据旋转的性质得到OA=OB,∠BOD=60°,易证得Rt△OAC≌Rt△BOD,OD=AC=-

a,BD=OC=-3a,于是有AE=OC-OD=-3a+

a,BE=BD-AC=-3a+

a,即AE=BE,则△ABE为等腰直角三角形,利用等腰直角三角形的性质得到3

-

=

(-3a+

a),求出a=1,确定A点坐标为(3,-

),然后把A(3,-

)代入函数y=

即可得到k的值.
解答:作AC⊥x轴与C,BD⊥x轴于D,AE⊥BD于E点,如图,
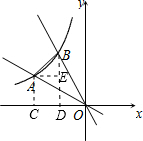
点A在直线y=-

x上,可设A点坐标为(3a,-

a),
在Rt△OAC中,OC=-3a,AC=-

a,
∴OA=
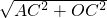
=-2

a,
∴∠AOC=30°,
∵直线OA绕O点顺时针旋转30°得到OB,
∴OA=OB,∠BOD=60°,
∴∠OBD=30°,
∴Rt△OAC≌Rt△BOD,
∴OD=AC=-

a,BD=OC=-3a,
∵四边形ACDE为矩形,
∴AE=OC-OD=-3a+

a,BE=BD-AC=-3a+

a,
∴AE=BE,
∴△ABE为等腰直角三角形,
∴AB=

AE,即3

-

=

(-3a+

a),
解得a=1,
∴A点坐标为(3,-

),
而点A在函数y=

的图象上,
∴k=3×(-

)=-3

.
故答案为-3

.
点评:本题考查了反比例函数综合题:点在反比例函数图象上,则点的横纵坐标满足其解析式;利用勾股定理、旋转的性质以及等腰直角三角形的性质进行线段的转换与计算.

 如图,函数
如图,函数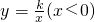 的图象与直线
的图象与直线 交于A点,将直线OA绕O点顺时针旋转30°,交函数
交于A点,将直线OA绕O点顺时针旋转30°,交函数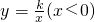 的图象于B点,若线段
的图象于B点,若线段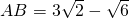 ,则k=________.
,则k=________.
 a),则OC=-3a,AC=-
a),则OC=-3a,AC=- a,利用勾股定理计算出OA=-2
a,利用勾股定理计算出OA=-2 a,得到∠AOC=30°,再根据旋转的性质得到OA=OB,∠BOD=60°,易证得Rt△OAC≌Rt△BOD,OD=AC=-
a,得到∠AOC=30°,再根据旋转的性质得到OA=OB,∠BOD=60°,易证得Rt△OAC≌Rt△BOD,OD=AC=- a,BD=OC=-3a,于是有AE=OC-OD=-3a+
a,BD=OC=-3a,于是有AE=OC-OD=-3a+ a,BE=BD-AC=-3a+
a,BE=BD-AC=-3a+ a,即AE=BE,则△ABE为等腰直角三角形,利用等腰直角三角形的性质得到3
a,即AE=BE,则△ABE为等腰直角三角形,利用等腰直角三角形的性质得到3 -
- =
= (-3a+
(-3a+ a),求出a=1,确定A点坐标为(3,-
a),求出a=1,确定A点坐标为(3,- ),然后把A(3,-
),然后把A(3,- )代入函数y=
)代入函数y= 即可得到k的值.
即可得到k的值.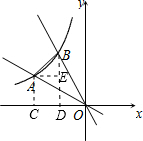
 x上,可设A点坐标为(3a,-
x上,可设A点坐标为(3a,- a),
a), a,
a,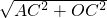 =-2
=-2 a,
a, a,BD=OC=-3a,
a,BD=OC=-3a, a,BE=BD-AC=-3a+
a,BE=BD-AC=-3a+ a,
a, AE,即3
AE,即3 -
- =
= (-3a+
(-3a+ a),
a), ),
), 的图象上,
的图象上, )=-3
)=-3 .
. .
.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案 8、男、女运动员在100m直道的相对两端同时起跑,往返练习跑步,测得男运动员每百米跑12s,女运动员每百米跑15s,如上如图所示的实线和虚线分别为这两个运动员所跑路程s(m)与时间t(s)之间的函数图象,请根据图象回答:
8、男、女运动员在100m直道的相对两端同时起跑,往返练习跑步,测得男运动员每百米跑12s,女运动员每百米跑15s,如上如图所示的实线和虚线分别为这两个运动员所跑路程s(m)与时间t(s)之间的函数图象,请根据图象回答: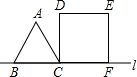 如图,(单位:cm)边长为10cm的等边△ABC以1cm/s的速度沿直线L向边长为10cm的正方形CDEF的方向移动,直到点B与点F重合,△ABC与正方形CDEF重叠部分的面积S关于平移动时间t的函数图象可能是( )
如图,(单位:cm)边长为10cm的等边△ABC以1cm/s的速度沿直线L向边长为10cm的正方形CDEF的方向移动,直到点B与点F重合,△ABC与正方形CDEF重叠部分的面积S关于平移动时间t的函数图象可能是( )
 从甲、乙两题中选做一题即可.如果两题都做,只以甲题计分.
从甲、乙两题中选做一题即可.如果两题都做,只以甲题计分. 明理由.
明理由.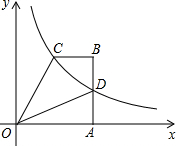 直角梯形OABC中,BC∥OA,∠OAB=90°,OA=4,腰AB上有一点D,AD=2,四边形ODBC的面积为6,建立如图所示的直坐标系,反比例函数y=
直角梯形OABC中,BC∥OA,∠OAB=90°,OA=4,腰AB上有一点D,AD=2,四边形ODBC的面积为6,建立如图所示的直坐标系,反比例函数y= 探索函数y=x+
探索函数y=x+