
【题目】某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)参加调查的人数共有 人;
(2)将条形图补充完整;
(3)求在扇形图中表示“其它球类”的扇形的圆心角的度数.

科目:初中数学 来源: 题型:
【题目】两艘专业救援船A,B同时收到信息,前往被困船只C所在海域实施救援任务,被困船只C位于救援船A的北偏东60°的方向上,位于救援船B的北偏西30°的方向上,船B在船A正东方向120海里处.
(1)求被困船只C到A、B两船所在直线的距离;
(2)若救援船A,救援船B分别以60海里/时,50海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达C处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是面积为 ![]() 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 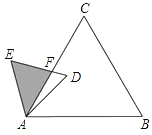
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为![]()
小红列出不完整的方程为![]()
(说明:其中“![]() ”表示运算符号,“
”表示运算符号,“![]() ”表示数字):
”表示数字):
(1)小明所列方程中![]() 表示的意义是________________________;
表示的意义是________________________;
小红所列方程中![]() 表示的意义是___________________________;
表示的意义是___________________________;
(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.
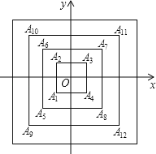
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
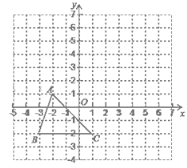
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP是△ABC的面积的2倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题发现)
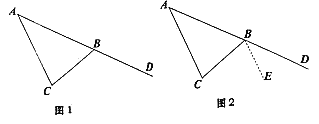
如图1,D是△ABC边AB延长线上一点,求证:∠A+∠C=∠CBD.
小白同学的想法是,过点B作 BE∥AC,从而将∠A和∠C转移到∠CBD处,使这三个角有公共顶点B,请你按照小白的想法,完成解答;
(问题解决)
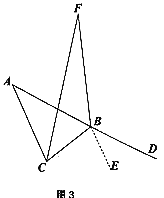
在上述问题的前提,,如图3,从点B引一条射线与∠ACB的角平分线交于点F,且∠CBF=∠D
BF,探究∠A与∠F的数量关系。在小白想法的提示下,小黑同学也想通过作平行线将∠A或∠F的位置进行转移,使两角有公共顶点,,请你根据小黑的想法或者学过的知识解决此问题。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com