
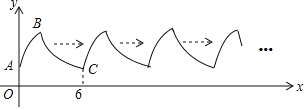
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分;曲线BC是双曲线y=![]() 的一部分.由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2026,n)均在该抛物线上,则m+n=_____.
的一部分.由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2026,n)均在该抛物线上,则m+n=_____.
【答案】9
【解析】
依据题意可得,A,C之间的水平距离为6,点Q与点P的水平距离为8,A,B之间的水平距离为2,双曲线解析式为y=![]() ,依据点P'、点B离x轴的距离相同,都为6,即点P的纵坐标m=6,点Q″、点Q'离x轴的距离相同,都为3,即点Q的纵坐标n=3,即可得到m+n的值.
,依据点P'、点B离x轴的距离相同,都为6,即点P的纵坐标m=6,点Q″、点Q'离x轴的距离相同,都为3,即点Q的纵坐标n=3,即可得到m+n的值.
由图可得,A,C之间的水平距离为6,
2018÷6=336…2,
由抛物线y=﹣x2+4x+2可得,顶点B(2,6),即A,B之间的水平距离为2,
∴点P'、点B离x轴的距离相同,都为6,即点P的纵坐标m=6,
由抛物线解析式可得AO=2,即点C的纵坐标为2,
∴C(6,2),
∴k=2×6=12,
∴双曲线解析式为y=![]() ,
,
2026﹣2018=8,故点Q与点P的水平距离为8,
∵点P'、Q″之间的水平距离=(2+8)﹣(2+6)=2,
∴点Q″的横坐标=2+2=4,
∴在y=![]() 中,令x=4,则y=3,
中,令x=4,则y=3,
∴点Q″、点Q'离x轴的距离相同,都为3,即点Q的纵坐标n=3,
∴m+n=6+3=9,
故答案为:9.



 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C,D为![]() 上的点,且
上的点,且![]() =
=![]() ,延长AD,BC相交于点E,连接OD交AC于点F.
,延长AD,BC相交于点E,连接OD交AC于点F.
(1)求证:△ABC≌△AEC;
(2)若OA=3,BC=4,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案所示图形是顶点在原点的抛物线的部分,方案二所示的图形是射线, 设推销员销售产品的数量为![]() (件),付给推销员的月报酬为
(件),付给推销员的月报酬为![]() (元),
(元),
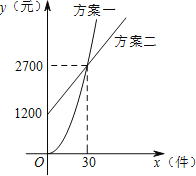
(1)请直接写出两种方案中![]() 关于
关于![]() 的函数关系式:方案一: ,方案二: ;
的函数关系式:方案一: ,方案二: ;
(2)当销售量达到多少件时,两种方案的月报酬差额将达到![]() 元?
元?
(3)若公司决定改进“方案二”:基本工资![]() 元,每销售件产品再增加报酬
元,每销售件产品再增加报酬![]() 元,当推销员销售量达到
元,当推销员销售量达到![]() 件时,方案二的月报酬不低于方案一的月报酬,求
件时,方案二的月报酬不低于方案一的月报酬,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了120千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加![]() 小时,求m的值.
小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() ,连接
,连接![]() ,
,![]() ,两条线段所在的直线交于点
,两条线段所在的直线交于点![]() .
.
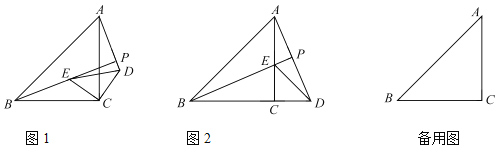
(1)线段![]() 与
与![]() 有何数量关系和位置关系,请说明理由.
有何数量关系和位置关系,请说明理由.
(2)若已知![]() ,
,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,
①如图2,当点![]() 恰好落在
恰好落在![]() 的延长线上时,求
的延长线上时,求![]() 的长;
的长;
②在旋转一周的过程中,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B两点,与y轴交于点C(0,3),抛物线的顶点在直线x=1上.
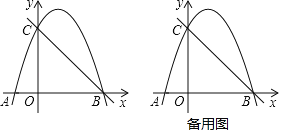
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P做PQ∥y轴交BC与点Q,当点P在何位置时,线段PQ的长度有最大值?
(3)点M在x轴上,点N在抛物线对称轴上,是否存在点M,点N,使以点M,N,C,B为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为弧AD的中点,连接CE交AB于点F,且BF=BC.

(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,![]() =
=![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
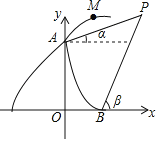
【题目】如图是某导弹发射车在山顶A处进行射击训练的示意图,点A在y轴上,与原点O的距离是8百米(为了计算方便,我们把本题中的距离用百米作单位).此导弹发射车在A处进行某个角度的射击训练,点M是导弹向右上射出后某时刻的位置.忽略空气阻力,实验表明:导弹射出t秒时,点M,A的水平距离是vt百米,点M与x轴(水平)的竖直距离是(8+vt﹣5t2)百米(v的值由发射者设定).在点A和x轴上的点B处观测射击目标P的仰角分别是a和β,OB=3百米,tanα=![]() .tanβ=
.tanβ=![]() .
.
(1)若v=7,完成下列问题:
①当点M,A的水平距离是7百米时,点M到x轴的距离是 百米;
②设点M坐标为(x,y),求y与x的关系式(不必写x的取值范围).
(2)按(1)的射击方式,能否命中目标P?请说明理由.
(3)目标以m百米/秒的速度从点P向右移动,当v![]() 时,若能使目标被击中,求m的取值范围.
时,若能使目标被击中,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com