
分析 (1)设A厂单独完成需要x天,B厂单独完成需要y天,根据“先由A厂生产30天,剩下的B厂生产20天可完成,或先由B厂生产30天,剩下的A厂可用15天完成”,即可得出关于$\frac{1}{x}$、$\frac{1}{y}$的二元一次方程组,解之即可得出结论;
(2)设选择A厂每天需付的工程款为m元,选择B厂每天需付的工程款为n元,根据“先由A厂生产30天,剩下的B厂生产20天可完成,共需支付工程款81000元;若先由B厂生产30天,剩下的A厂可用15天完成,共需支付工程款81000元”,即可得出关于m、n的二元一次方程组,解之即可得出m、n的值,依此可求出A、B两厂单独完成所需费用,设两厂合作完成,A厂生产a天,所需总费用为w元,则B厂生产(40-$\frac{2}{3}$a)天,根据总费用=工程费+技术员工资及午餐费,即可得出w关于a的函数关系式,根据一次函数的性质即可求出w的最小值,再将其与88200、85800比较后即可得出结论.
解答 解:(1)设A厂单独完成需要x天,B厂单独完成需要y天,
根据题意得:$\left\{\begin{array}{l}{\frac{30}{x}+\frac{20}{y}=1}\\{\frac{30}{y}+\frac{15}{x}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{\frac{1}{x}=\frac{1}{60}}\\{\frac{1}{y}=\frac{1}{40}}\end{array}\right.$,
∴x=60,y=40,
经检验,x=60、y=40符合题意.
答:A厂单独完成需要60天,B厂单独完成需要40天.
(2)设选择A厂每天需付的工程款为m元,选择B厂每天需付的工程款为n元,
根据题意得:$\left\{\begin{array}{l}{30m+20n=81000}\\{15m+30n=81000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1350}\\{n=2025}\end{array}\right.$,
∴选择A厂每天需付的工程款为1350元,选择B厂每天需付的工程款为2025元.
∴A厂单独完成需要费用为(1350+120)×60=88200(元),
B厂单独完成需要费用为(2025+120)×40=85800(元).
设两厂合作完成,A厂生产a天,所需总费用为w元,则B厂生产(40-$\frac{2}{3}$a)天,
根据题意得:当a≤40-$\frac{2}{3}$a,即a≤24时,w=1350a+2025(40-$\frac{2}{3}$a)+120×(40-$\frac{2}{3}$a)=-80a+85800,
此时,当a=24时,w取最小值,最小值为83880;
当a≥40-$\frac{2}{3}$a,即a≥24时,w=1350a+2025(40-$\frac{2}{3}$a)+120×a=120a+81000,
此时,当a=24时,w取最小值,最小值为83880.
∵88200>85800>83880,
∴A、B两厂每厂生产24天时,公司花费最少,最少金额为83880元.
点评 本题考查了二元一次方程组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据数量关系,找出w关于a的函数关系式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
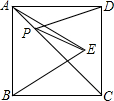 如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6.
如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
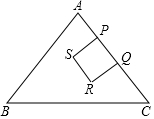 如图,在△ABC中,AB=AC=5,BC=6,P、Q两点同时从点A出发,点P沿AC边运动,速度为每秒1个单位:点Q沿A→C→B运动,速度为每秒2个单位,以PQ为边,在PQ左侧作正方形PQRS(P、Q、R、S按顺时针方向标记).设点P的运动时间为t(秒),正方形PQRS与△ABC的重叠部分的面积为S(平方单位).
如图,在△ABC中,AB=AC=5,BC=6,P、Q两点同时从点A出发,点P沿AC边运动,速度为每秒1个单位:点Q沿A→C→B运动,速度为每秒2个单位,以PQ为边,在PQ左侧作正方形PQRS(P、Q、R、S按顺时针方向标记).设点P的运动时间为t(秒),正方形PQRS与△ABC的重叠部分的面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com