
【题目】直线![]() ∥
∥![]() ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
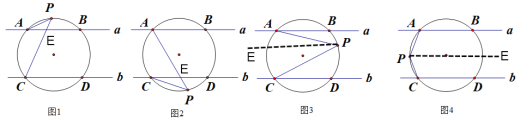
(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .

【答案】(1)∠PCD=∠P+∠PAB;(2)∠PAB=∠P+∠PCD;(3)见解析;(4)∠PAB+∠P+∠PCD=360°.
【解析】
(1)方法一:设AB、PC相交于点E,由外角性质得:∠PEB=∠P+∠PAB,又因为a∥b,所以∠PEB=∠PCD,从而求解;方法二:过点P作PE∥AB;
(2)方法一:设AP、CD相交于点E,理由同(1)得∠PED=∠P+∠PCD,又因为a∥b,所以∠PED=∠PAB,从而求解;方法二:过点P作PE∥AB;
(3) 过点P作PE∥a,因为a∥b,所以PE∥b,所以∠PAB=∠APE,∠∠PCD =∠EPC,
又因为∠APC=∠APE+∠CPE,所以∠APC=∠PAB+∠PCD;
(4) ∠PAB+∠P+∠PCD=360°. 过点P作PE∥a,因为a∥b,所以PE∥b,所以∠PAB+∠APE=180°,∠PCD+∠CPE=180°,即∠PAB+∠APE+∠PCD+∠CPE=360°,从而求解;
解 :(1)∠PCD=∠P+∠PAB;
理由:设AB、PC相交于点E,由外角性质得:∠PEB=∠P+∠PAB,
∵a∥b,∴∠PEB=∠PCD,
∴∠PCD=∠P+∠PAB;
(2)∠PAB=∠P+∠PCD;
理由:设AP、CD相交于点E,理由同(1)得∠PED=∠P+∠PCD,
又∵a∥b,∴∠PED=∠PAB,
∴ ∠PAB=∠P+∠PCD ;
(3)过点P作PE∥a,∵a∥b,∴PE∥b,
∴∠PAB=∠APE,∠∠PCD =∠EPC,
∵∠APC=∠APE+∠CPE
∴∠APC=∠PAB+∠PCD;;
(4) ∠PAB+∠P+∠PCD=360°
理由:过点P作PE∥a,∵a∥b,∴PE∥b,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°
∴∠PAB+∠APE+∠PCD+∠CPE=360°
即∠PAB+∠APC+∠PCD=360°.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC=______°,∠DEC=______°;点D从B向C运动时,∠BDA逐渐变______(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,![]() 是边长为
是边长为![]() 的等边三角形,作
的等边三角形,作![]() 与
与![]() 关于点
关于点![]() 成中心对称,再作
成中心对称,再作![]() 与
与![]() 关于点
关于点![]() 成中心对称,如此作下去,则
成中心对称,如此作下去,则![]() .(
.(![]() 是正整数)的顶点
是正整数)的顶点![]() 的坐标是___________________.
的坐标是___________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:

(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足![]() ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
(1)求C点坐标;
(2)如图2,连接DE,若DE![]() AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
(3)如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中,![]() 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
的大小是否发生变化,若不变,求出其值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
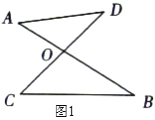
【题目】如图![]() ,线段
,线段![]() 、
、![]() 相交于
相交于![]() ,连结
,连结![]() 、
、![]() ,我们把形如图
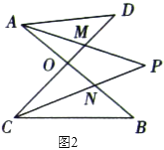
,我们把形如图![]() 的图形称之为“
的图形称之为“![]() ”字形,如图
”字形,如图![]() ,在图
,在图![]() 的条件下,
的条件下,![]() 和
和![]() 的平分线
的平分线![]() 和
和![]() 相交于点
相交于点![]() ,并且与
,并且与![]() 、
、![]() 分别相交于
分别相交于![]() 、
、![]() ,试解答下列问题:
,试解答下列问题:
(1)在图![]() 中,请直接写出
中,请直接写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系:__________
之间的数量关系:__________
(2)仔细观察,在图![]() 中“
中“![]() ”字形的个数:______个;
”字形的个数:______个;
(3)图![]() 中,当
中,当![]() 度,
度,![]() 度时,求
度时,求![]() 的度数.
的度数.
(4)图![]() 中
中![]() 和
和![]() 为任意角时,其它条件不变,试问
为任意角时,其它条件不变,试问![]() 与
与![]() 、
、![]() 之间存在着怎样的数量关系?(直接写出结果,不必证明)
之间存在着怎样的数量关系?(直接写出结果,不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com