
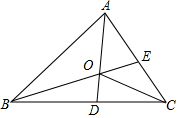
 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:分析 根据角平分线的性质可对①进行判断;利用三角形的角平分线相交于一点可对④进行判断;根据三角形内心的性质可对③进行判断;根据角平分线的定义和三角形的内角和可对②⑤进行判断.
解答 解:∵AD是△ABC的角平分线,
∴AD不一定垂直BC,所以①错误;
∵AD和BE是△ABC的角平分线,
∴CO平分∠BOC,所以④正确;
∴∠AOC=180°-∠OAC-∠OCA=180°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠BCA=180°-$\frac{1}{2}$(180°-∠ABC)=90°+$\frac{1}{2}$∠ABC,所以②正确;
∵点O为△ABC的内心,
∴OB、OC、OD不一定都相等,所以③错误;
∵∠AOE=∠OBA+∠OAB,
∴∠AOE+∠DCO=∠OBA+∠OAB+∠DCO=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$×180°=90°,所以⑤正确.
故答案为②④⑤.
点评 本题考查了三角形内角和定理:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.记住三角形内角和是180°


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
 如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.
如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
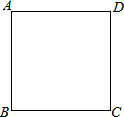 如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 工序 时间 模型 | 打磨(A组) | 组装(B组) |
| 模型甲 | 9分钟 | 5分钟 |
| 模型乙 | 6分钟 | 11分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
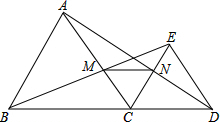 如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com