
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E. 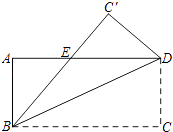
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
【答案】
(1)解:△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形
(2)解:设DE=x,则BE=x,AE=8﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8﹣x)2=x2,
解得:x=5,
所以S△BDE= ![]() DE×AB=
DE×AB= ![]() ×5×4=10
×5×4=10
【解析】(1)由折叠可知,∠CBD=∠EBD,再由AD∥BC,得到∠CBD=∠EDB,即可得到∠EBD=∠EDB,于是得到BE=DE,等腰三角形即可证明;(2)设DE=x,则BE=x,AE=8﹣x,在Rt△ABE中,由勾股定理求出x的值,再由三角形的面积公式求出面积的值.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】1.下列方程中,关于x的一元二次方程是( )
A. ax2+bx+c=0B. x2-x(x+7)=0C. 2x2-y-1=0D. x2-2x-3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 有两边和一角相等的两个三角形全等 B. 有一角相等的两个等腰三角形全等
C. 有一边相等的两个等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
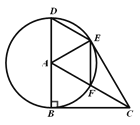
【题目】在Rt△ABC中,∠ABC=90°,以点A为圆心,AB为半径,作⊙A交AC于点F,交BA的延长线于点D,过点D作AC的平行线交⊙A于点E,连接AE、CE,EF.
⑴求证:CE⊥AE;
⑵当∠CAB等于多少度时,四边形ADEF为菱形,并给于证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
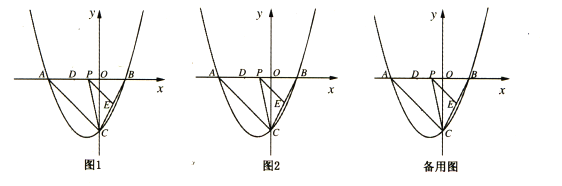
【题目】如图,抛物线![]() 与y轴交于点C(0,-4),与x轴交于点A、B,且B点的坐标为(2,0).
与y轴交于点C(0,-4),与x轴交于点A、B,且B点的坐标为(2,0).
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
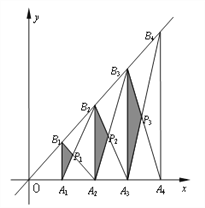
【题目】如图,已知A1、A2、……、An、An+1是x轴上的点,且OA1=A1A2=A2A3=……=AnAn+1=1,分别过点A1、A2、……、An、An+1作x轴的垂线交直线y=2x于点B1、B2、……、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、……、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、……、Pn,△A1B1P1、△A2B2P2、……、△AnBnPn的面积依次为S1、S2、……、Sn,则Sn为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com