
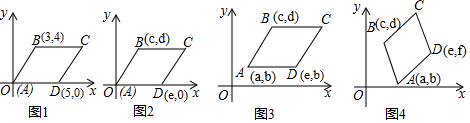
分析 (1)①根据平行四边形的性质:对边平行且相等,得出图2,3中顶点C的坐标分别是(e+c,d),(c+e-a,d);
②菱形绕原点逆时针依照(90°,2)旋转,根据定义即可解决问题;
(2)①分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,分别过A,D作AE⊥BB1于E,DF⊥CC1于点F.在平行四边形ABCD中,CD=BA,根据内角和定理,又∵BB1∥CC1,可推出∠EBA=∠FCD,△BEA≌△CFD.依题意得出AF=DF=a-c,BE=CF=d-b.设C(x,y).由e-x=a-c,得x=e+c-a.由y-f=d-b,得y=f+d-b.继而推出点C的坐标.
②根据定义,利用①中的结论即可解决问题;
(3)①在平行四边形ABCD中,CD=BA,同理证明△BEA≌△CFD(同(2)证明).然后推出AF=DF=a-c,BE=CF=d-b.又已知C点的坐标为(m,n),e-m=a-c,故m=e+c-a.由n-f=d-b,得出n=f+d-b.
②根据旋转的定义,即可解决问题;
解答 解:(1)①由题意可得出:图1,图2,图3中的顶点C的坐标,它们分别是(8,4),(e+c,d),(c+e-a,d).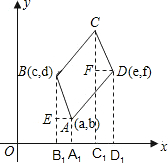
故答案为:(8,4),(e+c,d),(c+e-a,d).
②菱形绕原点逆时针依照(90°,2)旋转后点C对应的点C1的坐标分别是(-8,16),(-2d,2e+2c),(-2d,2c+2e-2a)
故答案为(-8,16),(-2d,2e+2c),(-2d,2c+2e-2a).
(2)①如图所示:分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,
分别过A,D作AE⊥BB1于E,DF⊥CC1于点F.
在平行四边形ABCD中,CD=BA,
又∵BB1∥CC1,
∴∠EBA+∠ABC+∠BCF=∠ABC+∠BCF+∠FCD=180度.
∴∠EBA=∠FCD.
在△BEA和△CFD中
$\left\{\begin{array}{l}{∠AEB=∠DFC}\\{∠EBA=∠FCD}\\{AB=CD}\end{array}\right.$,
∴△BEA≌△CFD(AAS).
∴AE=DF=a-c,BE=CF=d-b.
设C(x,y).
由e-x=a-c,得x=e+c-a.
由y-f=d-b,得y=f+d-b.
∴C(e+c-a,f+d-b).
②菱形绕原点逆时针依照(90°,2)旋转后对应的C1的坐标为(2b-2f-2d,2e+2c-2a)
(3)①由图1,2,3可得出:m=c+e-a,n=d+f-b.或m+a=c+e,n+b=d+f.
故答案为:m=c+e-a,n=d+f-b.
②由图1,2,3可得出:无论C点在哪个位置,绕原点逆时针依照(90°,n)旋转可得:x2=-ny1,y2=nx1,
故答案为x2=-ny1,y2=nx1.
点评 此题主要考查了平行四边形的性质,平面直角坐标系内的坐标,平行线的性质、旋转变换、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
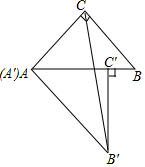 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )| A. | 3$\sqrt{3}$ | B. | 6 | C. | 3$\sqrt{2}$ | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 将油滴入水中,油会浮在水面上 | |
| B. | 车辆随机到达一个路口,遇到红灯 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 掷一枚质地均匀的硬币,一定正面向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
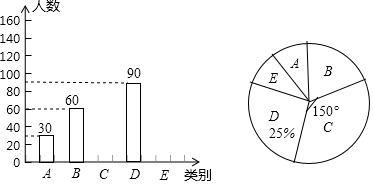
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com