
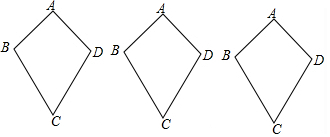
分析 (1)连接AC,判定出△ABC≌△ADC,即可;
(2)利用三角形的一条直线将三角形分成两个面积相等的三角形即可作出图形;
(3)先求出四边形ABCD的面积,即可得出四边形ABQD的面积,从而求出QM,再用平行线分线段成比例定理求出BM,即可得出DM,最后用勾股定理即可.
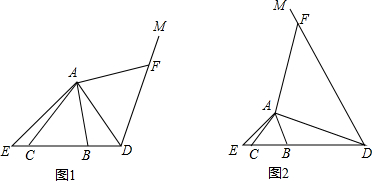
解答 解:(1)如图1,
连接 AC,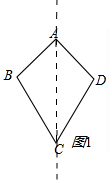
证明:在△ABC 和△ADC 中,$\left\{\begin{array}{l}{AB=AD}\\{CB=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC,
∴S△ABC=S△ADC
∴AC 所在的直线平分筝形的面积.
(2)如图2,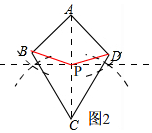
作出AC 的中点P,连接BP、DP,折线B-P-D 将筝形ABCD 面积二等分.
证明:在△ABC 中,
∵P 为AC 边中点,
∴AP=CP,
∴S△APB=S△CPB=$\frac{1}{2}$ S△ABC,
同理:S△APD=S△CPD=$\frac{1}{2}$S△ADC,
∵S△ABC=S△ADC
∴S△APD+S△APB=S△CPB+S△CPD
即四边形ABPD 的面积=四边形BCDP 的面积
∴折线B-P-D将筝形ABCD面积二等分.
(3)如图3,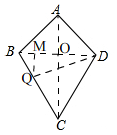
连接BD,AC交于点O.在BC上取一点Q,过Q作QM⊥BD,
∵在△BCO 和△DCO 中,
由(1)知,∠BCA=∠DCA,
在△BCO和△DCO中,$\left\{\begin{array}{l}{BC=DC}\\{∠BCA=∠DCA}\\{OC=OC}\end{array}\right.$
∴△BCO≌△DCO,
∴∠BOC=∠DOC,
∴AC⊥BD,
在Rt△ABD 中,BD=$\sqrt{2}$AB=4,
∴DO=BO=OA=2,
在Rt△BCO 中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=4$\sqrt{2}$,
∴S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD×(AO+CO)=$\frac{1}{2}$×4×(2+4$\sqrt{2}$)=4+8$\sqrt{2}$,
∵在一条过点D的直线将筝形ABCD的面积二等分,
∴S四边形ABQD=$\frac{1}{2}$S四边形ABCD=2+4$\sqrt{2}$,
∵S△ABD=$\frac{1}{2}$×BD×OA=4,
∴S△QBD=$\frac{1}{2}$BD×QM=$\frac{1}{2}$×4×QM=2QM=S四边形ABQD-S△ABD=2+4$\sqrt{2}$-4=4$\sqrt{2}$-2,
∴QM=2$\sqrt{2}$-1,
∵QM∥CO.
∴$\frac{BM}{BO}=\frac{QM}{CO}$,
∴$\frac{BM}{2}=\frac{2\sqrt{2}-1}{4\sqrt{2}}$,
∴BM=$\frac{4-\sqrt{2}}{4}$,
∴DM=BD-BM=$\frac{12+\sqrt{2}}{4}$
在Rt△MQD 中,DQ2=DM2+MQ2=$\frac{145-20\sqrt{2}}{8}$.
点评 此题是四边形综合题,主要考查了等腰三角形的性质,三角形的中线,几何作图,勾股定理,求出四边形ABCD的面积是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:解答题
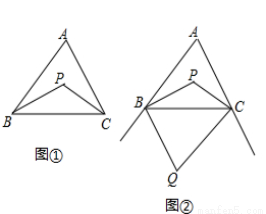
如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
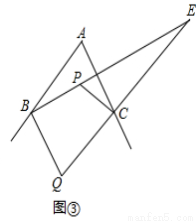
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校七年级3月月考数学试卷(解析版) 题型:单选题
如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠ACB相等的角有( )
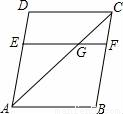
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com