
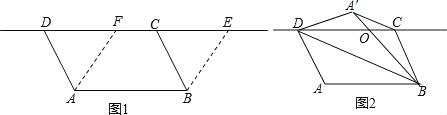
����Ŀ����ͼ1����ABEF�У�AB=2��AF��AB���ֽ��߶�EF��ֱ��EF���ƶ������ƶ������У����߶�EF�Ķ�Ӧ�߶�ΪCD������AD��BC��
��1���������ƶ������У������ı��ε�˵������ȷ���� B
A��������ֲ��� B��ֻ��һ��ʱ��Ϊ����
C��ֻ��һ��ʱ��Ϊ���� D���ܳ��ı�
��2���������ƶ������У���ͼ2��������ABD����BD�۵��õ���A��BD����A�����C���غϣ���A��B��CD�ڵ�O��
������A��C��BDƽ������˵�����ɣ�
������A����D��B��CΪ������ı����Ǿ��Σ��ҶԽ��ߵļн�Ϊ60������AD�ij���
���𰸡�(1)��B��(2)���������ɼ�����������1��![]()
��������
���������(1)������ƽ�Ƶ����ʽ����жϼ��ɣ�(2)�������ݶ��۵����ʵó���Ӧ�ߺͽ���ȣ��ٸ���ƽ���ߵ��ж���ɣ� �����ݾ��ε����ʺ͵ȱ������ε����ʽ��з������
���������(1)����Ϊƽ�ƣ�AB���ֲ��䣬��AB��CD��ľ��벻�䣬�����ı���ABCD��������䣬��A��ȷ����AD��CDʱ���ı���ABCD�����Ǿ��Σ���C��ȷ����ΪAD�ij����б仯�������ı���ABCD���ܳ��ı䣬��D��ȷ��
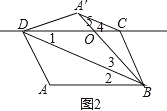
(2)������A'C��BD���������£�
��ͼ2����ABEF�ɵã�AB=CD��AB��CD���ָ��ݶ��ۿ�֪AB=A'B����3=��2����A'B=CD����1=��3��
��OD=OB����OA'=OC�� ���4=��5���ߡ�BOD=��A'OC�����4+��5=��1+��3�� ����1=��4�� ��A'C��BD��
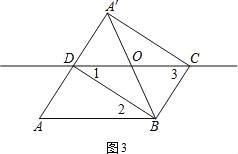
������ͼ3������֪CD=AB=2����1=��2����A=��3�����ı���A'DBC����ʱ������DBC=90����OA'=OD=OB=OC=1��
����A'OD=60��������DOB=120�������1=30�������2=30������A=��3=60�������ADB=90����
����Rt��ADB��AD=![]() AB=1��
AB=1��
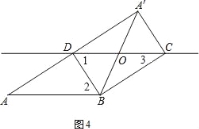
����DOB=60������ͼ4��������ODBΪ�������Σ����2=��1=60������A=��3=30��BD=OD=1�����ADB=90��
����Rt��ADB��tan��2=![]() ����AD=BDtan��2=1tan60��=
����AD=BDtan��2=1tan60��=![]() ��
��
���Ͽɵã�AD�ij�Ϊ1��![]() ��
��


 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ��Ϊ����ӪҵԱ�Ļ����ԣ�����ʵ��Ŀ�����������ÿ������Ŀ�����������Ž��𣮸õ�ͳ����ÿλӪҵԱǰ������¾����۶������������ݵ�ƽ��������������λ�����ֱ�Ϊ22��15��18����λ����Ԫ����������һ�����ҵ�ӪҵԱ���ܴﵽ������Ŀ�꣬�������۶Ϊ_____��Ԫ��Ϊ���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ�������
A. ��4b+b=��3b B. 2x2+2x3=4x5 C. 5x��x=5 D. a2b��ab2=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�����оٰ����조������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 8 |
��3�� | 35��x��40 | 16 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������㷨��������ôһ���⣺��ֱ����˰���ʮ�IJ���ֻ�Ƴ�������ʮ�����ʳ��༸�Σ�����˼�ǣ�һ�������ص����Ϊ864ƽ������ֻ֪�����ij������60���������ij��ȿ����˶��ٲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У��������ĶԳ�ͼ�ε��ǣ�������
A.ƽ���ı���B.ԲC.�ȱ�������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=BC��AD��BC�ڵ�D����EΪAC�е���BEƽ�֡�ABD������BE��AD�ڵ�F����BF=AC������D��DG��AB����AC�ڵ�G��
��֤��
��1����BAD=2��DAC
��2��EF=EG��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com