Question

15．如图，抛物线y=-x²+12x-30的顶点为A，对称轴AB与x轴交于点B．在x轴上方的抛物线上有C、D两点，它们关于AB对称，并且C点在对称轴的左侧，CB⊥DB．
（1）求出此抛物线的对称轴和顶点A的坐标；
（2）在抛物线的对称轴上找出点Q，使它到A、C两点的距离相等，并求出点Q的坐标；
（3）延长DB交抛物线于点E，在抛物线上是否存在点P，使得△DEP的面积等于△DEC的面积？若存在，请你直接写出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）将已知的抛物线解析式化为顶点式，即可得到抛物线对称轴方程以及顶点的坐标．
（2）此小题首先要求出点C的坐标；对于Rt△CBD来说，C、D关于抛物线对称轴对称，则CB=BD，那么△CBD是等腰直角三角形，若设抛物线对称轴与CD的交点为G，那么△BCG也是等腰直角三角形，可先设出点C的横坐标，再由Rt△BCG的特殊形状表示出点C的纵坐标，代入抛物线的解析式中即可求出点C的坐标．抛物线对称轴已知，设出点Q的纵坐标后，依坐标系两点间的距离公式表示出CQ、AQ的长，由CQ=AQ列出方程求出点Q的坐标；
（3）若△DEP、△DEC的面积相等，那么点P与点C到直线DE的距离相同；
①过点C作平行于DE的直线，该直线与抛物线的交点为符合条件的点P，此时点P、C到直线DE的距离相同；
②过点D作DF∥BC，交x轴于点F，此时四边形DCBF是平行四边形，那么DF⊥DE，且DF=BC，那么过点F与直线DE平行的直线与抛物线的交点也是符合条件的点P．

解答 解：（1）∵y=-x²+12x-30=-（x-6）²+6，
∴此抛物线的对称轴为x=6，
顶点A的坐标（6，6）；

（2））∵C、D关于AB对称，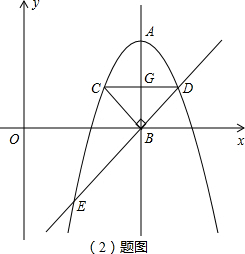
∴BC=BD，CD∥x轴；
又∵CB⊥DB，
∴△BCD是等腰直角三角形，
∴∠DCB=45°，即△BCG为等腰直角三角形，CG=BG；
设点C的横坐标为a，则CG=6-a，BG=CG=6-a，即C（a，6-a），代入y=-x²+12x-30，得：
6-a=-a²+12a-30，解得：a₁=4、a₂=9（舍）
∴C（4，2）；
设Q（6，m），则AQ=6-m，CQ=$\sqrt{{2}^{2}+（m-2）^{2}}$，
∵AQ=CQ，
∴6-m=$\sqrt{{2}^{2}+（m-2）^{2}}$，
解得m=$\frac{7}{2}$
∴Q（6，$\frac{7}{2}$）；

（3）设直线DE的解析式：y=kx+b，代入D（8，2）、B（6，0），
得：$\left\{\begin{array}{l}{8k+b=2}\\{6k+b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=1}\\{b=-6}\end{array}\right.$，
故直线DE：y=x-6；
若△DEP的面积等于△DEC的面积，则点C、P到直线DE的距离相等；
①过点C作直线l₁∥DE，可设其解析式为：y=x+b₁，代入C（4，2）解得：b₁=-2；
即：直线l₁ y=x-2，联立抛物线的解析式有：
$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+12x-30}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=2}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{2}=7}\\{{y}_{2}=5}\end{array}\right.$，
故P₁（7，5）．
②过点D作DF∥CB，交x轴于点F，则四边形DCBF为平行四边形，且有：DF⊥DE，BF=CD=4，即F（10，0）；
过点F作直线l₂∥DE，同①易求得直线l₂：y=x-10，联立抛物线的解析式，
有：$\left\{\begin{array}{l}{y=x-10}\\{y=-{x}^{2}+12x-30}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{11+\sqrt{41}}{2}}\\{{y}_{1}=\frac{-9+\sqrt{41}}{2}}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{2}=\frac{11-\sqrt{41}}{2}}\\{{y}_{2}=\frac{-9-\sqrt{41}}{2}}\end{array}\right.$
故P₂（$\frac{11+\sqrt{41}}{2}$，$\frac{-9+\sqrt{41}}{2}$）、P₃（$\frac{11-\sqrt{41}}{2}$，$\frac{-9-\sqrt{41}}{2}$）．
综上，符合条件的点P的坐标为P₁（7，5）、P₂（$\frac{11+\sqrt{41}}{2}$，$\frac{-9+\sqrt{41}}{2}$）、P₃（$\frac{11-\sqrt{41}}{2}$，$\frac{-9-\sqrt{41}}{2}$）．

点评 此题考查了二次函数、等腰直角三角形、平行四边形等综合知识；（2）题中，由抛物线的对称性得出△BCD的特殊形状，进而得出C点的坐标是解题的突破口；最后一题，找出经过点P且与直线DE平行的两条直线是解题的关键，容易漏解．