
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣAΘ®©¹1Θ§0Θ©ΓΔCΘ®4Θ§0Θ©Θ§BCΓΆx÷α”ΎΒψCΘ§«“ACΘΫBCΘ§≈ΉΈοœΏyΘΫx2+bx+cΨ≠ΙΐAΓΔBΝΫΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΒψE «œΏΕΈAB…œ“ΜΕ·ΒψΘ®≤Μ”κAΓΔB÷ΊΚœΘ©Θ§ΙΐΒψEΉςx÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψFΘ§Β±œΏΕΈEFΒΡ≥ΛΕ»Ήν¥σ ±Θ§«σΒψEΒΡΉχ±ξΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΓςEFP «“‘EFΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωΥυ”–ΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫx2©¹2x©¹3ΘΜΘ®2Θ©ΒψEΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜΘ®3Θ©¥φ‘ΎΘ§P1Θ®
Θ©ΘΜΘ®3Θ©¥φ‘ΎΘ§P1Θ®![]() Θ§
Θ§![]() Θ©Θ§P2Θ®
Θ©Θ§P2Θ®![]() Θ§
Θ§![]() Θ©Θ§P3Θ®
Θ©Θ§P3Θ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σΒΟΒψAΒΡΉχ±ξΘ§»ΜΚσΫΪΒψAΚΆΒψBΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΩ…ΒΟΒΫΙΊ”ΎbΓΔcΒΡΖΫ≥ΧΉιΘ§¥”ΕχΩ…«σΒΟbΓΔcΒΡ÷ΒΘΜ
Θ®2Θ©…ηΒψEΒΡΉχ±ξΈΣΘ®xΘ§x+1Θ©Θ§‘ρΒψFΒΡΉχ±ξΈΣFΘ®xΘ§x2©¹2x©¹3Θ©Θ§‘ρΩ…ΒΟΒΫEF”κxΒΡΚ· ΐΙΊœΒ ΫΘ§άϊ”Ο≈δΖΫΖ®Ω…«σΒΟEFΒΡΉν¥σ÷Β“‘ΦΑΒψEΒΡΉχ±ξΘΜ
Θ®3Θ©¥φ‘ΎΘ§Ζ÷ΝΫ÷÷«ιΩωΩΦ¬«ΘΚΘ®iΘ©ΙΐΒψEΉςaΓΆEFΫΜ≈ΉΈοœΏ”ΎΒψPΘ§…ηΒψPΘ®mΘ§m2©¹2m©¹3Θ©Θ§”…EΒΡΉίΉχ±ξ”κPΉίΉχ±ξœύΒ»Ν–≥ωΙΊ”ΎmΒΡΖΫ≥ΧΘ§«σ≥ωΖΫ≥ΧΒΡΫβΒΟΒΫmΒΡ÷ΒΘ§»ΖΕ®≥ωP1Θ§P2ΒΡΉχ±ξΘΜΘ®ΔΔΘ©ΙΐΒψFΉςbΓΆEFΫΜ≈ΉΈοœΏ”ΎP3Θ§…ηP3Θ®nΘ§n2©¹2n©¹3Θ©Θ§ΗυΨίFΒΡΉίΉχ±ξ”κPΒΡΉίΉχ±ξœύΒ»Ν–≥ωΙΊ”ΎnΒΡΖΫ≥ΧΘ§«σ≥ωΖΫ≥ΧΒΡΫβΒΟΒΫnΒΡ÷ΒΘ§«σ≥ωP3ΒΡΉχ±ξΘ§Ήέ…œΒΟΒΫΥυ”–¬ζΉψΧβ“βPΒΟΉχ±ξΘ°
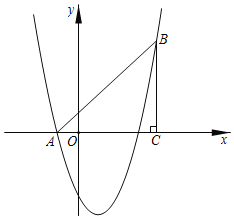
Θ®1Θ©ΓΏAΘ®©¹1Θ§0Θ©ΓΔCΘ®4Θ§0Θ©Θ§
ΓύOAΘΫ1Θ§OCΘΫ4Θ§
ΓύACΘΫ5Θ§
ΓΏBCΓΆx÷α”ΎΒψCΘ§«“ACΘΫBCΘ§
ΓύBΘ®4Θ§5Θ©Θ§
ΫΪΒψAΚΆΒψBΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚ![]() Θ§ΫβΒΟΘΚbΘΫ©¹2Θ§cΘΫ©¹3Θ°
Θ§ΫβΒΟΘΚbΘΫ©¹2Θ§cΘΫ©¹3Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣyΘΫx2©¹2x©¹3Θ°
Θ®2Θ©ΓΏ÷±œΏABΨ≠ΙΐΒψAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§5Θ©Θ§
…η÷±œΏABΒΡΫβΈω ΫΈΣyΘΫkx+bΘ§
Γύ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏABΒΡΫβΈω ΫΈΣΘΚyΘΫx+1Θ§
ΓΏΕΰ¥ΈΚ· ΐyΘΫx2©¹2x©¹3Θ§
Γύ…ηΒψEΘ®tΘ§t+1Θ©Θ§‘ρFΘ®tΘ§t2©¹2t©¹3Θ©Θ§
ΓύEFΘΫΘ®t+1Θ©©¹Θ®t2©¹2t©¹3Θ©ΘΫ©¹Θ®t©¹![]() Θ©
Θ©![]() Θ§
Θ§
ΓύΒ±tΘΫ![]() ±Θ§EFΒΡΉν¥σ÷ΒΈΣ
±Θ§EFΒΡΉν¥σ÷ΒΈΣ![]() Θ§
Θ§
ΓύΒψEΒΡΉχ±ξΈΣΘ®![]() Θ©Θ°
Θ©Θ°
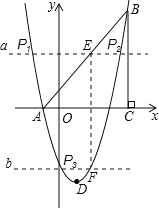
Θ®3Θ©¥φ‘ΎΘ§Ζ÷ΝΫ÷÷«ιΩωΩΦ¬«ΘΚ
Θ®ΔΓΘ©ΙΐΒψEΉςaΓΆEFΫΜ≈ΉΈοœΏ”ΎΒψPΘ§…ηΒψPΘ®mΘ§m2©¹2m©¹3Θ©Θ§
Γύ![]()
![]() Θ§
Θ§
Γύm1=![]() Θ§m2=
Θ§m2=![]()
ΓύP1Θ®![]() Θ§
Θ§![]() Θ©Θ§P2Θ®
Θ©Θ§P2Θ®![]() Θ§
Θ§![]() Θ©
Θ©
Θ®ΔΔΘ©ΙΐΒψFΉςbΓΆEFΫΜ≈ΉΈοœΏ”ΎP3Θ§…ηP3Θ®nΘ§n2©¹2n©¹3Θ©
‘ρ”–ΘΚn2©¹2n©¹3ΘΫ©¹![]()
Γύn1=![]() , n2=
, n2=![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
ΓύP3Θ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘ§ ΙΓςEFP «“‘EFΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–ΈΥυ”–ΒψPΒΡΉχ±ξΈΣΘΚP1Θ®![]() Θ§
Θ§![]() Θ©Θ§P2Θ®
Θ©Θ§P2Θ®![]() Θ§
Θ§![]() Θ©Θ§P3Θ®
Θ©Θ§P3Θ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=kx+bΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσΫΜ”ΎAΘ®©¹2Θ§1Θ©Θ§BΘ®1Θ§nΘ©ΝΫΒψΘ°
ΒΡΆΦœσΫΜ”ΎAΘ®©¹2Θ§1Θ©Θ§BΘ®1Θ§nΘ©ΝΫΒψΘ°
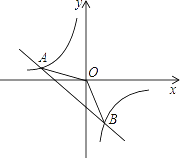
Θ®1Θ© ‘»ΖΕ®…œ ωΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©«σΓςAOBΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐ![]() Θ®
Θ®![]() Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§Ε‘≥Τ÷αΈΣ
Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§Ε‘≥Τ÷αΈΣ![]() Θ§Ηχ≥ωœ¬Ν–Ϋα¬έΘΚΔΌ
Θ§Ηχ≥ωœ¬Ν–Ϋα¬έΘΚΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔή
ΘΜΔή![]() Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”–Θ® Θ©
Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”–Θ® Θ©
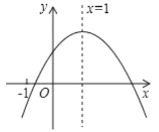
A.4ΗωB.3ΗωC.2ΗωD.1Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“–Θ≤ίΗυΈΡ―ß…γΈΣΝΥΝΥΫβ―ß…ζΩΈΆβ‘ΡΕΝ«ιΩωΘ§≥ι―υΒς≤ιΝΥ≤ΩΖ÷―ß…ζΟΩ÷ή”Ο”ΎΩΈΆβ‘ΡΕΝΒΡ ±ΦδΘ§Ιΐ≥Χ»γœ¬ΘΚ
ΐΨί ’Φ·Θ§¥”»Ϊ–ΘΥφΜζ≥ι»Γ20Οϊ―ß…ζΘ§Ϋχ––ΝΥΟΩ÷ή”Ο”ΎΩΈΆβ‘ΡΕΝ ±ΦδΒΡΒς≤ιΘ§ ΐΨί»γœ¬Θ®ΒΞΈΜΘΚΖ÷Θ©
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
’ϊάμœ¬Ζ÷ΕΈ’ϊάμ―υ±Ψ ΐΨί≤Δ≤Ι»Ϊ±μΗώΘ°
ΩΈΆβ‘ΡΕΝ ±ΦδxΘ®Ζ÷Θ© | 0ΓήxΘΦ40 | 40ΓήxΘΦ80 | 80ΓήxΘΦ120 | 120ΓήxΘΦ160 |
Β»ΦΕ | D | C | B | A |
»Υ ΐ | 3 | ΓΓ ΓΓ | 8 | ΓΓ ΓΓ |
Ζ÷Έω ΐΨίΘΚ≤Ι»Ϊœ¬Ν–±μΗώ÷–ΒΡΆ≥ΦΤΝΩΘ°
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ |
80 | ΓΓ ΓΓ | ΓΓ ΓΓ |
ΒΟ≥ωΫα¬έΘΚ
Θ®1Θ©”Ο―υ±Ψ÷–ΒΡΆ≥ΦΤΝΩΙάΦΤΈ“–Θ―ß…ζΟΩ÷ή”Ο”ΎΩΈΆβ‘ΡΕΝ ±ΦδΒΡ«ιΩωΒ»ΦΕΈΣΓΓ ΓΓΘΜ
Θ®2Θ©ΦΌ…ηΤΫΨυ‘ΡΕΝ“Μ±ΨΩΈΆβ ιΒΡ ±ΦδΈΣ160Ζ÷÷”Θ§«κΡψ―Γ‘ώ―υ±Ψ÷–ΒΡΤΫΨυ ΐΙάΦΤΈ“–Θ―ß…ζΟΩ»Υ“ΜΡξΘ®Α¥52÷ήΦΤΥψΘ©ΤΫΨυ‘ΡΕΝΕύ…Ό±ΨΩΈΆβ ιΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
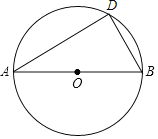
ΓΨΧβΡΩΓΩ»γΆΦAB «Γ―OΒΡ÷±ΨΕΘ§ΒψDΈΣΓ―O…œ»Έ“β“ΜΒψΝ§Ϋ”ADΘ§DBΘ°
Θ®1Θ©‘ΎADΒΡ…œΖΫΉςΓœDAC=ΓœDABΘ§ΫΜΝ”ΜΓAO”ΎΒψCΘ°Θ®≥ΏΙφΉςΆΦΘ§±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ–¥ΉςΖ®Θ©
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§»τΓœDAB=30ΓψΘ§Ν§Ϋ”CDΘ§ODΘ°«σ÷ΛΘΚΥΡ±Ώ–ΈAODCΈΣΝβ–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
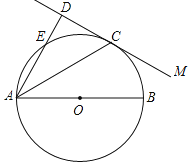
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§÷±œΏMC”κΓ―Oœύ«–”ΎΒψCΘ°ΙΐΒψAΉςMCΒΡ¥ΙœΏΘ§¥ΙΉψΈΣDΘ§œΏΕΈAD”κΓ―OœύΫΜ”ΎΒψEΘ°
Θ®1Θ©«σ÷ΛΘΚAC «ΓœDABΒΡΤΫΖ÷œΏΘΜ
Θ®2Θ©»τABΘΫ10Θ§ACΘΫ4![]() Θ§«σAEΒΡ≥ΛΘ°
Θ§«σAEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
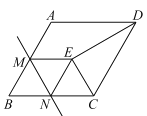
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΝβ–Έ![]() ÷–Θ§
÷–Θ§![]() ΈΣ±Ώ
ΈΣ±Ώ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§![]() ΈΣ±Ώ
ΈΣ±Ώ![]() …œ“ΜΕ·ΒψΘ®≤Μ”κ
…œ“ΜΕ·ΒψΘ®≤Μ”κ![]() ÷ΊΚœΘ©Θ§ΫΪ
÷ΊΚœΘ©Θ§ΫΪ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() ’έΒΰΘ§ ΙΒψ
’έΒΰΘ§ ΙΒψ![]() ¬δ‘ΎΒψ
¬δ‘ΎΒψ![]() ¥ΠΘ§Ν§Ϋ”
¥ΠΘ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§Β±
Θ§Β±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§![]() ΒΡ≥ΛΈΣ____________.
ΒΡ≥ΛΈΣ____________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“εΘΚΕ‘”ΎΗχΕ®ΒΡΝΫΗωΚ· ΐΘ§»Έ»ΓΉ‘±δΝΩxΒΡ“ΜΗω÷ΒΘ§Β±xΘΦ0 ±Θ§ΥϋΟ«Ε‘”ΠΒΡΚ· ΐ÷ΒΜΞΈΣœύΖ¥ ΐΘΜΒ±xΓί0 ±Θ§ΥϋΟ«Ε‘”ΠΒΡΚ· ΐ÷ΒœύΒ»Θ§Έ“Ο«≥Τ’β―υΒΡΝΫΗωΚ· ΐΜΞΈΣœύΙΊΚ· ΐΘ°άΐ»γΘΚ“Μ¥ΈΚ· ΐy=x©¹1Θ§ΥϋΒΡœύΙΊΚ· ΐΈΣ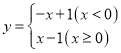 Θ°
Θ°
Θ®1Θ©“―÷ΣΒψAΘ®©¹5Θ§8Θ©‘Ύ“Μ¥ΈΚ· ΐy=ax©¹3ΒΡœύΙΊΚ· ΐΒΡΆΦœσ…œΘ§«σaΒΡ÷ΒΘΜ
Θ®2Θ©“―÷ΣΕΰ¥ΈΚ· ΐ![]() Θ°
Θ°
ΔΌΒ±ΒψBΘ®mΘ§![]() Θ©‘Ύ’βΗωΚ· ΐΒΡœύΙΊΚ· ΐΒΡΆΦœσ…œ ±Θ§«σmΒΡ÷ΒΘΜ
Θ©‘Ύ’βΗωΚ· ΐΒΡœύΙΊΚ· ΐΒΡΆΦœσ…œ ±Θ§«σmΒΡ÷ΒΘΜ
ΔΎΒ±©¹3ΓήxΓή3 ±Θ§«σΚ· ΐ![]() ΒΡœύΙΊΚ· ΐΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘΜ
ΒΡœύΙΊΚ· ΐΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘΜ
Θ®3Θ©‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψMΘ§NΒΡΉχ±ξΖ÷±πΈΣΘ®©¹![]() Θ§1Θ©Θ§Θ®
Θ§1Θ©Θ§Θ®![]() Θ§1}Θ©Θ§Ν§ΫαMNΘ°÷±Ϋ”–¥≥ωœΏΕΈMN”κΕΰ¥ΈΚ· ΐ
Θ§1}Θ©Θ§Ν§ΫαMNΘ°÷±Ϋ”–¥≥ωœΏΕΈMN”κΕΰ¥ΈΚ· ΐ![]() ΒΡœύΙΊΚ· ΐΒΡΆΦœσ”–ΝΫΗωΙΪΙ≤Βψ ±nΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡœύΙΊΚ· ΐΒΡΆΦœσ”–ΝΫΗωΙΪΙ≤Βψ ±nΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() Θ§
Θ§![]() ‘ΎΖ¥±»άΐΚ· ΐ
‘ΎΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσ…œ‘ΥΕ·Θ§«“ Φ÷’±Θ≥÷œΏΕΈ
ΒΡΆΦœσ…œ‘ΥΕ·Θ§«“ Φ÷’±Θ≥÷œΏΕΈ![]() ΒΡ≥ΛΕ»≤Μ±δΘ°
ΒΡ≥ΛΕ»≤Μ±δΘ°![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΘ§Ν§Ϋ”
ΒΡ÷–ΒψΘ§Ν§Ϋ”![]() Θ°‘ρœΏΕΈ
Θ°‘ρœΏΕΈ![]() ≥ΛΕ»ΒΡΉν–Γ÷Β «_____(”ΟΚ§
≥ΛΕ»ΒΡΉν–Γ÷Β «_____(”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ)Θ°
ΒΡ¥ζ ΐ Ϋ±μ Ψ)Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com