
分析 (1)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果;
(3)原式先计算乘方运算,再计算乘法运算即可得到结果;
(4)原式利用单项式乘以多项式法则计算即可得到结果;
(5)原式利用多项式乘以多项式法则计算即可得到结果;
(6)原式利用平方差公式,完全平方公式计算即可得到结果;
(7)原式利用完全平方公式及平方差公式计算即可得到结果.
解答 解:(1)原式=4-1+9=12;
(2)原式=(100+1)×(100-1)=10000-1=9999;
(3)原式=(-2xy3)•4x2y2•($\frac{1}{4}$x2y)=-2x5y6;
(4)原式=5x3-10x2-5x;
(5)原式=-2x3-3x2+10x+15;
(6)原式=b2-4a2-a2-9b2+6ab=-5a+6ab-8b2;
(7)原式=(a-3b)2-c2=a2-6ab+9b2-c2.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷(解析版) 题型:解答题
(本小题满分9分)
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4),点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动,点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动,连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相较于点D,BD与y轴交于点E,连接PE,设P运动时间为t(s).
(1)∠PBD的度数为__________,点D的坐标为______________(用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)△POE的周长是否随时间t的变换而变化?若变化,说明理由;若不变化,试求这个定值.


备用图
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+b)(2b-a) | B. | (a+1)(-a-1) | C. | (3x-y)(-3x+y) | D. | (-m-n)(-m+n) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
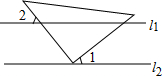 如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )
如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角互补的平行四边形是矩形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
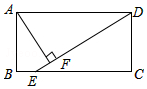 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )| A. | △AFD≌△DCE | B. | 2AF=AD | C. | AB=AF | D. | BE=AD-DF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5,2.4 | B. | 2.5,$\sqrt{7}$ | C. | 2.5,2.5 | D. | 2.5,2.4 |
查看答案和解析>>
科目:初中数学 来源:2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷(解析版) 题型:单选题
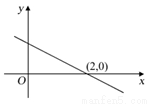
函数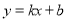 (
(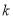 、
、 为常数,
为常数, 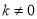 )图象如图所示,则关于
)图象如图所示,则关于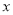 的不等式
的不等式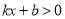 的解集为( )
的解集为( )
A. 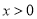 B.
B. 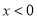 C.
C. 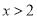 D.
D. 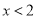
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com