
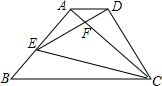
 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD; ②△ACD∽△BCE; ③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为$\frac{3}{8}$.其中正确的结论是①②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD; ②△ACD∽△BCE; ③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为$\frac{3}{8}$.其中正确的结论是①②④⑤. 分析 ①首先根据等腰三角形的性质得到∠ACB=∠DCE=45°,从而得到∠ACB-∠ACE=∠DCE-∠ACE,进而得到结论:∠ECB=∠DCA正确;
②利用两对角对应相等的三角形相似证得结论△ACD∽△BCE即可;
④证得△BEC∽△ADC后得到∠DAC=∠B=45°,从而得到∠DAC=∠BCA=45°,即AD∥BC;
③由④知:△EAD与△BEC不相似,故③错误;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;由④的△BEC∽△ADC知:当AD最长时,BE也最长;故梯形ABCD面积最大时,E、A重合,此时EC=AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$,故S梯形ABCD=$\frac{1}{2}$(1+$\frac{1}{2}$)×$\frac{1}{2}$=$\frac{3}{8}$,从而判定是否正确即可;
解答 解:∵△ABC、△DCE都是等腰Rt△,
∴AB=AC=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$,CD=DE=$\frac{\sqrt{2}}{2}$CE;
∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB-∠ACE=∠DCE-∠ACE;
即∠ECB=∠DCA;故①正确;
②∵△ABC与△CDE,均为等腰直角三角形,
∴∠B=∠ACB=∠DEC=∠DCE,
∴∠BCE=∠ACD,
∵∠ADC=∠BEC,
∴△ACD∽△BCE,
故②正确;
④∵$\frac{CD}{EC}$=$\frac{AC}{BC}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{CD}{AC}$=$\frac{CE}{BC}$;
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,即AD∥BC,故④正确;
③由④知:∠DAC=45°,则∠EAD=135°;
∠BEC=∠EAC+∠ECA=90°+∠ECA;
∵∠ECA<45°,∴∠BEC<135°,即∠BEC<∠EAD;
因此△EAD与△BEC不相似,故③错误;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;
△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$;
故S梯形ABCD=$\frac{1}{2}$(1+$\frac{1}{2}$)×$\frac{1}{2}$=$\frac{3}{8}$,故⑤正确;
因此本题正确的结论是①②④⑤,
故答案为:①②④⑤.
点评 此题主要考查了等腰直角三角形的性质、平行线的判定、相似三角形的判定和性质、图形面积的求法等知识,综合性强,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com