
����Ŀ����ƽ��ֱ������ϵ�У�������y= ![]() x2��
x2�� ![]() x��2��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����D���C����x��Գƣ�����BD
x��2��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����D���C����x��Գƣ�����BD
��1�����A��B��C�����꣮
��2������Pʱx���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l�����������ڵ�M����ֱ��BD�ڵ�N
�ٵ���P���߶�OB���˶�ʱ������O��B�غϣ�����mΪ��ֵʱ���߶�MN�ij������˵����ʱ�ı���DCMN�Ƿ�Ϊƽ���ı���
�ڵ���P���˶������У��Ƿ���ڵ�M��ʹ��BDM����BDΪֱ�DZߵ�ֱ�������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��y= ![]() x2��
x2�� ![]() x��2�У���y=0�ɵ�0=
x��2�У���y=0�ɵ�0= ![]() x2��
x2�� ![]() x��2�����x=��1��x=4��
x��2�����x=��1��x=4��
��A����1��0����B��4��0����
��y= ![]() x2��
x2�� ![]() x��2�У���x=0�ɵ�y=��2��
x��2�У���x=0�ɵ�y=��2��
��C��0����2����
��2��
�١�D��C����x��Գƣ�
��D��0��2������B��4��0����
�����ֱ��BD����ʽΪy=kx+2����B���������ɵ�4k+2=0�����k=�� ![]() ��
��
��ֱ��BD����ʽΪy=�� ![]() x+2��
x+2��
��P��m��0����
��N��m���� ![]() m+2����M��m��
m+2����M��m�� ![]() m2��
m2�� ![]() m��2����
m��2����
��P���߶�OB�ϣ�
��M��x���·���
��MN=�� ![]() m+2����
m+2���� ![]() m2��
m2�� ![]() m��2��=��
m��2��=�� ![]() m2+m+4=��
m2+m+4=�� ![]() ��m��1��2+
��m��1��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
�൱m=1ʱ��MN�����ֵ�����ֵΪ ![]() ��
��
��CD=4��MN��
���ı���DCMN����ƽ���ı��Σ�
�ڡߵ�P���߶�OB���˶���
���M�ڵ������ޣ�
���MDB��90�㣬
����BDM����BDΪֱ�DZߵ�ֱ��������ʱ��ֻ��MB��BD����ͼ��
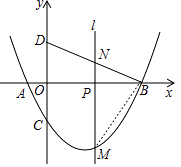
��P��m��0������M��m�� ![]() m2��
m2�� ![]() m��2������B��4��0����D��0��2����
m��2������B��4��0����D��0��2����
��BP=4��m��PM=�� ![]() m2+
m2+ ![]() m+2��OB=4��OD=2��
m+2��OB=4��OD=2��
�ߡ�MBD=90�㣬
���OBD+��PBM=��ODB+��OBD=90�㣬
���ODB=��PMB��
���OBD�ס�PMB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����m=3��m=4����ȥ����
�����m=3��m=4����ȥ����
��M��������3����2����
����������1�����������߽���ʽ�������A��B��C�����ꣻ��2���ٿ����ֱ��BD�Ľ���ʽ������m�ɱ�ʾ��MN�ij���������ö��κ������������MN�����ֵ�����ж�MN��CD�Ƿ���ȼ��ɣ����������ֻ֪��BM��BD�������M������꣬�Ӷ��ɱ�ʾ��BP��MP�ij������á�OBD�ס�PMB���ɵõ�����M������ķ��̣��Ӷ������M������꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���Լ���ƽ���ı��ε��ж������ʵ����⣬�˽���һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε������


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AO=10��AB=8���ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ����D��3��10����E��0��6����������y=ax2+bx+c����O��D��C���㣮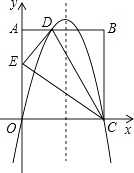
��1���������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ��������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ�ı���MENC��ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ־Ը���Ŷ��������ڹ�����һ��ţ�̵���Ϧ���족����Ժο�ʹ¹����ˣ������ÿ�����˷�5�У���ʣ��38�У������ÿ�����˷�6�У������һ�����˲���5�У������ٷֵ�һ�У�
��1���辴��Ժ��x�����ˣ�������ţ�̹��ж��ٺУ����ú�x�Ĵ���ʽ��ʾ����
��2���þ���Ժ�����ж��������ˣ�����ж��������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��40cm�Ľ�������������س�x��7cm��С�κ�y��9cm��С�Σ�ʣ�ಿ�������ϴ�������ʹ�������٣���������x��yӦ�ֱ�Ϊ�� ��
A.x=1��y=3
B.x=4��y=1
C.x=3��y=2
D.x=2��y=3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڡ�ǰϦ��ij������6000Ԫ�������ɻ��������к�ܿ����꣬��������7500Ԫ�����ڶ���ͬ���Ļ�������֪�ڶ��������������ǵ�һ��������1.5������ÿ�������Ľ��۱ȵ�һ���Ľ�����5Ԫ�����һ������ÿ�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����6�ű�����ȫ��ͬ��ֽ�ƽ���������Ϸ����Ϸ�������£�������ֱ��������1��3��6������ֽ�Ƹ�С����������ֱ��������2��4��5������ֽ�Ƹ�С����С��С���ֱ�ֽ�Ʊ��泯�ϣ��Ӹ��Ե�����ֽ����������һ�ţ�������������ſ�Ƭ�ϵ�������ӣ������Ϊż������С����ʤ�������Ϊ��������С����ʤ��
��1��С���鵽��������6��ֽ�Ƶĸ���Ϊ��
��2��������״ͼ���б��ķ�����С����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����һ��ͼ�Σ�����ͼ���й���2���ǣ�ͼ���й���6���ǣ�ͼ���й���11���ǣ�ͼ���й���17���ǣ��������˹��ɣ�ͼ�������ǵĿ����ǣ� ��
A.43
B.45
C.51
D.53
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=2��EΪBC�е㣬��������M��N�ֱ��ڱ�CD��AD���˶���MN=1������ABE����D��M��NΪ��������������ƣ���DM= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ��ǿɻ�����κ�ƽ���ı���ѧ�ߣ���֪ƽ���ı��ν϶̵ı������εı߳���ȣ�
��1����һ����ѧ��У�ijС��ѧ�������ε�һ����ƽ���ı��ν϶̱��غϣ���ƴ����ͼ1��ʾ��ͼ�Σ�AF������C������DE��AF�ڵ�M���۲췢�֣���M��DE���е㣮
��������λѧ���д����Ե�֤��˼·��
˼·1�������������ߣ�ֱ��֤������ȫ�ȣ�
˼·2����֤������ȫ�ȣ�����BD��AF�ڵ�H����
��ο������˼·��֤����M��DE���е㣨ֻ����һ�ַ���֤������
��2����ͼ2���ڣ�1����ǰ���£�����ABE=135��ʱ���ӳ�AD��EF���ڵ�N���� ![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£��� ![]() =k��kΪ����
=k��kΪ���� ![]() �ij�������ֱ���ú�k�Ĵ���ʽ��ʾ
�ij�������ֱ���ú�k�Ĵ���ʽ��ʾ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com