
【题目】如图,抛物线y=(x﹣1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标.
【答案】
(1)
解:把C(0,﹣3)代入y=(x﹣1)2+n,得,﹣3=(0﹣1)2+n,
解得n=﹣4,
∴抛物线的解析式为y=(x﹣1)2﹣4,
∴抛物线的对称轴为直线x=1,
∵点D与点C关于抛物线的对称轴对称,
∴点D的坐标为(2,﹣3)
(2)
解:连接PA、PC、PD
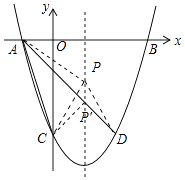
∵点D与点C关于抛物线的对称轴对称
∴PC=PD
∴AC+PA+PC=AC+PA+PD
∵AC为定值,PA+PD≥AD
∴当PA+PC的值最小,即A,P,D三点在同一直线上时△PAC的周长最小,
由y=(x﹣1)2﹣4=0解得,x1=﹣1,x2=3,
∵A在B的左侧,∴A(﹣1,0),
由A,D两点坐标可求得直线AD的解析式为y=﹣x﹣1,
当x=1时,y=﹣x﹣1=﹣2,
∴当△PAC的周长最小时,点P的坐标为(1,﹣2)
(3)
解:如图2中,
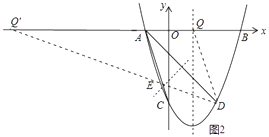
①作DQ∥AC交x轴于点Q,此时∠DQA=∠DAC,满足条件.
∵A(﹣1,0),C(0,﹣3),
∴直线AC的解析式为y=﹣3x﹣3,
∴直线QD的解析式为y=﹣3x+3,
令y=0得x=1,
∴Q(1,0).
②设线段AD的垂直平分线交AC于E,直线DE与x的交点为Q′,此时∠Q′DA=′CAD,满足条件,
∵直线AD的解析式为y=﹣x﹣1,
∴线段AD的中垂线是解析式为y=x﹣2,
由 ![]() 解得
解得 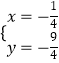 ,
,
∴E(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴直线DE的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
令y=0得到x=﹣7,
∴Q′(﹣7,0).
综上所述,Q点坐标为(1,0)或(﹣7,0)
【解析】(1)利用待定系数法即可求出n,利用对称性C、D关于对称轴对称即可求出点D坐标.(2)A,P,D三点在同一直线上时△PAC的周长最小,求出直线AD的解析式即可解决问题.(3)分两种情形①作DQ∥AC交x轴于点Q,此时∠DQA=∠DAC,满足条件.②设线段AD的垂直平分线交AC于E,直线DE与x的交点为Q′,此时∠Q′DA=′CAD,满足条件,分别求解即可.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】我市计划对某地块的1000m2区域进行绿化,由甲、乙两个工程队合作完成.已知甲队每天能完成绿化的面积是乙队的2倍;若两队分别各完成300m2的绿化时,甲队比乙队少用3天.
(1)求甲、乙两工程队每天能完成的绿化的面积;
(2)两队合作完成此工程,若甲队参与施工x天,试用含x的代数式表示乙队施工的天数y;
(3)若甲队每天施工费用是0.6万元,乙队每天为0.2万元,且要求两队施工的天数之和不超过16天,应如何安排甲、乙两队施工的天数,才能使施工总费用最低?并求出最低费用时的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__ __,∠XBC+∠XCB=__ __;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( ) 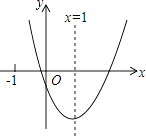
A.①②
B.①④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是_____度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_____等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师驾车从家出发到植物园赏花,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后加速行驶,到达植物园,参观结束后,张老师驾车一路匀速返回,其中x表示汽车从家出发后所用时间,y表示车离家的距离,下面能反映y与x的函数关系式的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com