
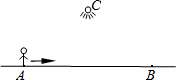
 如图,晚上小王从点A经过路灯C的正下方沿直线走到点B,他的影长y随他离点A之间的距离x的变化而变化,那么下列图象中能反映y与x之间的函数关系的是( )
如图,晚上小王从点A经过路灯C的正下方沿直线走到点B,他的影长y随他离点A之间的距离x的变化而变化,那么下列图象中能反映y与x之间的函数关系的是( )| A. |  | B. | 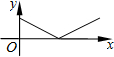 | C. | 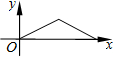 | D. | 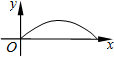 |
分析 等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
解答  解:设身高GE=h,CF=l,AF=a,
解:设身高GE=h,CF=l,AF=a,
当x≤a时,
在△OEG和△OFC中,
∠GOE=∠COF(公共角),∠AEG=∠AFC=90°,
∴△OEG∽△OFC,
∴$\frac{OE}{OF}$=$\frac{GE}{CF}$,
∴$\frac{y}{a-x}$=$\frac{h}{l}$,
∴y=-$\frac{h}{l}$x+$\frac{ha}{l}$,
∵a、h、l都是固定的常数,
∴自变量x的系数是固定值,
∴这个函数图象肯定是一次函数图象,即是直线;
∵影长将随着离灯光越来越近而越来越短,到灯下的时候,将是一个点,进而随着离灯光的越来越远而影长将变大.
故选:B.
点评 本题综合考查了中心投影的特点和规律.注意离点光源的远近决定影长的大小.


科目:初中数学 来源: 题型:解答题
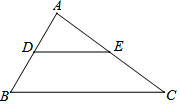 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°;
如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°; 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
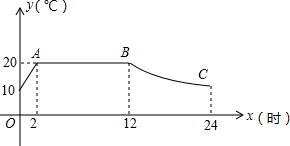 某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15~20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=$\frac{k}{x}$的一部分,请根据图中信息解答下列问题:
某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15~20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=$\frac{k}{x}$的一部分,请根据图中信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com