
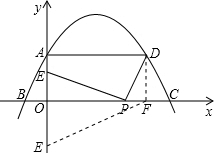
 (a>0)的图象与y轴交于点A,与x轴交于点B、C,过A点作x轴的平行线交抛物线于另一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.问题:
(a>0)的图象与y轴交于点A,与x轴交于点B、C,过A点作x轴的平行线交抛物线于另一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.问题: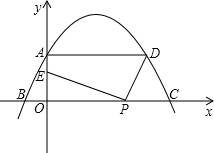
 ;
;
 ,
,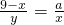 ,
, x2+
x2+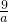 x;
x; ,
, =
= ,
, x2-
x2-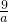 x;
x; x2+
x2+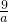 x,化为x2-9x+a2=0;
x,化为x2-9x+a2=0; .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
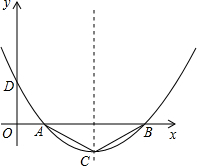 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,| 7 |
| 9 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com