
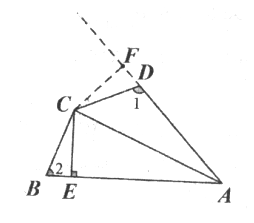
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

【答案】∠1+∠2=180°
【解析】
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件![]() ,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
猜想:∠1+∠2=180°
证明:过C点作CF⊥AD延长线于点F,
∵CE⊥AB,AC平分∠DAB,
∴CB=CF,
∠CEB=∠CFD=90°,
在Rt△CEA和Rt△CFA中
∵![]()
∴Rt△CEA≌Rt△CFA(HL),
∴AE=AF,
∵![]() ,
,
AE+AF=AF-FD+AE+BE,
∴FD=BE,
在△CEB和△CFD中
∵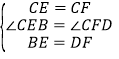
∴△CEB≌△CFD(SAS),
∴∠2=∠CDF,
∵∠CDF+∠1=180°,
∴∠1+∠2=180°.


科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2013年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中(如图每格一个单位),描出下列各点A(﹣2,﹣1),B(2,﹣1),C(2,2),D(3,2),E(0,3),F(﹣3,2),G(﹣2,2),A(﹣2,﹣1)并依次将各点连接起来,观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段FD和x轴有什么位置关系?点F和点D的坐标有什么特点?
查看答案和解析>>
科目:初中数学 来源: 题型:
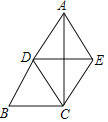
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com