
【题目】已知在![]() 中,
中, ![]() ,以
,以![]() 上的一点
上的一点![]() 为圆心,以
为圆心,以![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )如果
)如果![]() 是⊙
是⊙![]() 的切线,
的切线, ![]() 是切点,
是切点, ![]() 是
是![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)AC=4.
【解析】试题分析:(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;
(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
试题解析:(1)证明:连接DE,∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC,∵∠DAE=∠BAC,∴△ADE∽△ABC,∴ ![]() ,∴ACAD=ABAE;
,∴ACAD=ABAE;
(2)解:连接OD,∵BD是⊙O的切线,∴OD⊥BD,在RT△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°,同理∠BAC=30°,在RT△ABC中,AC=2BC=2×2=4.



 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
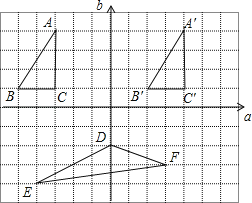
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
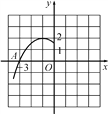
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).

A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )设抛物线的顶点为
)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 在直线
在直线![]() 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点![]() 使
使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了![]() 天完成,乙做另一部分用了
天完成,乙做另一部分用了![]() 天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
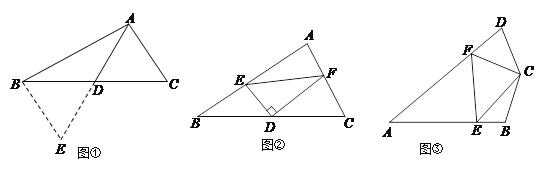
(1)如图①,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
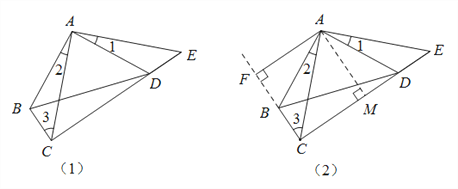
【题目】如图(1),在四边形ABCD中,已知∠ABC![]() ∠ADC
∠ADC![]() 180°,AB
180°,AB![]() AD,AB
AD,AB![]() AD,点E在CD的延长线上,∠1
AD,点E在CD的延长线上,∠1![]() ∠2.
∠2.
(1)求证:∠3![]() ∠E;
∠E;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,求证:CE![]() 2AF.
2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,∠A=50°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC的度数为( )

A. 130° B. 115° C. 110° D. 105°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com