
【题目】根据规定:距离高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
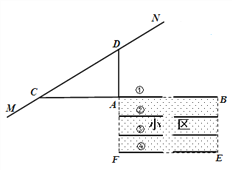
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°,AD=220.某人看中了①号楼A单元的一套住宅,但是感觉小区距离高铁轨道这么近,易受噪音污染,而售楼人员却说,虽然A单元离高铁轨道最近,但是AD长达220米,是达到设计要求的.
(1) 你认为售楼人员的话是否可信?为什么?
(2) 若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈61)
≈61)
【答案】(1)不可信,理由略; (2)5秒.
【解析】试题分析:(1)作过点A作AG⊥MN,垂足为G,根据三角函数可求AG的长,再与200米比较大小即可求解;
(2)在MN上找到点S、T,使得AS=AT=200米,根据勾股定理可求GT,根据三角函数可求ST,依此可求速度,进一步得到A单元用户受到影响的时间.
试题解析:(1)作过点A作AG⊥MN,垂足为G,
∵∠ACD=30°,DA⊥CA,
∴∠ADC=60°,
∵AD=220米,
∴AG=ADsin60°=110![]() ≈187<200,
≈187<200,
∴A单元用户会受到影响,售楼人员的说法不可信;
(2)在MN上找到点S、T,使得AS=AT=200米,
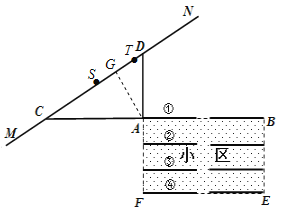
∴GT=GS=![]() 米,
米,
∴ST=2GT=20![]() ≈122米,
≈122米,
又∵速度V=![]() =70(米/秒),
=70(米/秒),
∴时间t=![]() =5秒,即受影响的时间为5秒.
=5秒,即受影响的时间为5秒.


科目:初中数学 来源: 题型:
【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 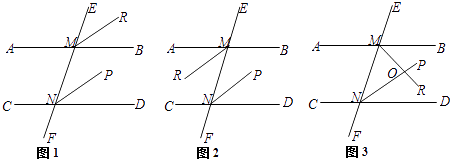
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是( )
A.(﹣4,0)
B.(6,0)
C.(﹣4,0)或(6,0)
D.(0,12)或(0,﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AC<AB.
(1) 用直尺和圆规作出一条过点A的直线l,使得点C关于直线l的对称点落在边AB上(不写作法,保留作图痕迹);
(2) 设直线l与边BC的交点为D,且∠C=2∠B,请你通过观察或测量,猜想线段AB、AC、CD之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣3)×(﹣ ![]() )÷(﹣1
)÷(﹣1 ![]() )
)
(2)48×( ![]() )﹣(﹣48)÷(﹣8)
)﹣(﹣48)÷(﹣8)
(3)(﹣1)2013﹣22﹣|﹣ ![]() |×(﹣10)2﹣19
|×(﹣10)2﹣19 ![]() ×19 (用简便方法计算)
×19 (用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列两个命题:①若两个角是对顶角,则这两个角相等;②若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形.说法正确的是( )
A.命题①正确,命题②不正确
B.命题①、②都正确
C.命题①不正确,命题②正确
D.命题①、②都不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com