
 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.
在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7. 分析 作AB的中点E,连接EM、CE,根据直角三角形斜边上的中线等于斜边的一半以及三角形的中位线定理求得CE和EM的长,然后在△CEM中根据三边关系即可求解.
解答 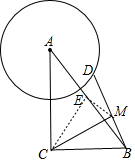 解:作AB的中点E,连接EM、CE.
解:作AB的中点E,连接EM、CE.
在直角△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵E是直角△ABC斜边AB上的中点,
∴CE=$\frac{1}{2}$AB=5.
∵M是BD的中点,E是AB的中点,
∴ME=$\frac{1}{2}$AD=2.
∴在△CEM中,5-2≤CM≤5+2,即2≤CM≤7.
∴最大值为7,
故答案为:7.
点评 本题考查了点与圆的位置关系、三角形的中位线定理的知识,要结合勾股定理、直角三角形斜边上的中线等于斜边的一半解答.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
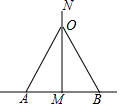 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)| A. | 14m | B. | 11m | C. | 13m | D. | 10m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 是原来的5倍 | C. | 是原来的$\frac{1}{5}$ | D. | 是原来的$\frac{1}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
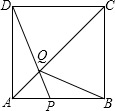 如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连结DP交AC于点Q.
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连结DP交AC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com