
【题目】对于反比例函数y=![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A. 它的图象分布在第一、三象限 B. 点(k,k)在它的图象上
C. 它的图象关于原点对称 D. 在每个象限内y随x的增大而增大
科目:初中数学 来源: 题型:
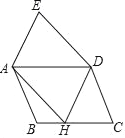
【题目】如图,将平行四边形ABCD绕点D旋转,点C落在BC上的点H处,点B恰好落在点A处,得平行四边形DHAE,若BH=2,CH=3,则DC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.
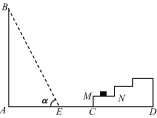
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
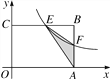
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠BAD是△ABC的一个外角,∠BAC、∠BAD的平分线分别交⊙O于点E、F.请你在图上连接EF.(1)证明:EF是⊙O的直径;(2)请你判断EF与BC有怎样的位置关系?并请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).

(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com