
����Ŀ�����꼶��ѧѧϰ����С����ѧ����ͼ�ε����ơ���һ�º��ֿɽ����������εĶ��塢�ж��Լ�������չ�����Ρ����ε�������ȥ���磺���ǿ��Զ��壺�����Ϳ�֮����ȵľ��������ƾ��Σ������ƾ���Ҳ�����µ����ʣ����ƾ��εĶԽ���֮�ȵ������Ʊȣ��ܳ��ȵ������Ʊȣ�����ȵ������Ʊȵ�ƽ���ȵȣ�����������ѧϰС�飬һͬ̽���������⣺
![]() д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
![]() ��ͼ��������
��ͼ��������![]() ����ֱ��
����ֱ��![]() ����ƽ�ƺ�õ�����
����ƽ�ƺ�õ�����![]() ����֤�����ı���
����֤�����ı���![]() �����Σ�������
������������![]() ����
����![]() ��
��
![]() ��
��![]() ������
������![]() �����������
�����������![]() �����һ�룬��ƽ�Ƶľ���
�����һ�룬��ƽ�Ƶľ���![]() �ij���
�ij���
���𰸡�![]() ��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������![]() ֤����������
֤����������![]() ��
��
��������
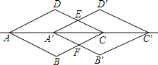
��1�������ı���ȣ�����һ���Ӧ����ȼ��ɣ���2���ɣ�1���Ľ��ۣ�������֪������DAB����D��A��B����֤�����ƣ���3����������ȵ������Ʊȵ�ƽ����A��C��������AA��.
![]() ��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
��һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ�������
![]() ����
����![]() ��
��![]() ����
����![]()
������![]() �Ľ��ۣ��õ�֤����
�Ľ��ۣ��õ�֤����
![]() ������
������![]() ����
����![]() ������
������![]() �����������
�����������![]() �����һ�룬
�����һ�룬
������![]() ������
������![]() �������Ϊ
�������Ϊ![]() ��
��
����Ӧ��֮��Ϊ![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ե�OΪԲ�ĵ�����ͬ��Բ�У���Բ����AB��СԲ�ڵ�C��D����ͼ����
��1����֤��AC=BD��
��2������Բ�İ뾶R=10��СԲ�İ뾶r=8����ԲO��ֱ��AB�ľ���Ϊ6����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ֧Ԯ�������裬�ƻ���![]() ��
��![]() �����ֵ����ͼ������ʷֱ�Ϊ60�ֺ�140�֣����мס��������м������ʷֱ�Ϊ120�ֺ�80�֣���֪�ס��������˵�
�����ֵ����ͼ������ʷֱ�Ϊ60�ֺ�140�֣����мס��������м������ʷֱ�Ϊ120�ֺ�80�֣���֪�ס��������˵�![]() ��
��![]() ���ص�ÿ�����ʵ��˷������ʾ��
���ص�ÿ�����ʵ��˷������ʾ��
�� | �� | |
| 20Ԫ/�� | 15Ԫ/�� |
| 25Ԫ/�� | 24Ԫ/�� |
��1������˵�![]() �صļ�������Ϊ
�صļ�������Ϊ![]() �֣������˷�
�֣������˷�![]() ��Ԫ������
��Ԫ������![]() ���֣��ĺ�����ϵʽ����д��
���֣��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����������˷ѣ���˵�����˷����ʱ�����ͷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��BC��CD�ֱ����O������E��F��G����AB��CD��OB=6cm��OC=8cm����
��1����BOC�Ķ�����
��2��BE+CG�ij���
��3����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪S��ABC��12��ADƽ�֡�BAC����AD��BD�ڵ�D����S��ADC��ֵ��( )

A. 10 B. 8 C. 6 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
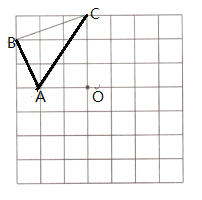
����Ŀ��������������ͼ�У���ÿ��С�����εı߳���1��![]() ��
��![]() ���ڵ�
���ڵ�![]() �Գƣ�
�Գƣ�
��1������![]() ��
��
��2��![]() ��
��![]() ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
��3����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() ����Сֵ�� ��
����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��4���������������⣺
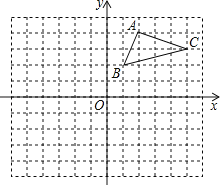
��1��������ABC����x��ԳƵ���A1B1C1����д����C1�����꣨�� ���� ����
��2������ABC����������ĺᡢ�����궼���ԩ�1���ֱ�õ���Ӧ��A2��B2��C2���뻭����A2B2C2����˵����A1B1C1����A2B2C2�Ƿ�����Գ�ͼ�Σ�����ǣ���ô���ǵĶԳ�����ʲô��������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
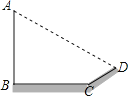
����Ŀ����ͼ��ij��С�����������µ��߸�AB��Ӱ���������µ�����CD�͵���BC�ϣ�����CD=8�ף�BC=20�ף�б��CD���¶ȱ�Ϊ1��![]() ���Ҵ�ʱ���1�˵�Ӱ��Ϊ2�ף�����߸˵ĸ߶�Ϊ�� ��
���Ҵ�ʱ���1�˵�Ӱ��Ϊ2�ף�����߸˵ĸ߶�Ϊ�� ��
A����14+2![]() ���� B��28�� C����7+
���� B��28�� C����7+![]() ���� D��9��
���� D��9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨��sin����x������sinx��cos����x����cosx��sin��x+y����sinx��cosy��cosx��siny���ݴ��ж����е�ʽ��������_________������ţ���
��cos����60��������cos60��=![]()
��sin75����sin��30��+45����=sin30�㡤cos45��+cos30�㡤sin45��=![]()
��sin2x��sin��x+x����sinx��cosx+cosx��sinx��2sinx��cosx��
��sin��x��y����sinx��cosy��cosx��siny��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com