
����Ŀ��ijУΪ���õ�����ѧ����Ȥ����չ����չ�γ��߰�ѡ�Ρ�����������˲���ѧ�����˽�������ϲ������Ŀ���ͣ���Ϊ�鷨��Χ�塢Ϸ�硢������4�ࣩ������ͳ�ƽ�����Ƴ���ͼ��������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��ϲ������Ŀ����Ƶ���ֲ���
��Ŀ���� | Ƶ�� | Ƶ�� |
�鷨�� | 18 | a |
���� | 14 | 0.28 |
ϲ���� | 8 | 0.16 |
������ | b | 0.20 |
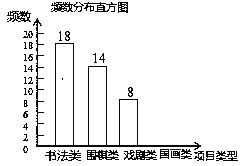
����������Ϣ����������⣺
��1��ֱ��д��Ƶ���ֲ�����a��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ȫУ����ѧ��1500�������Ƹ�У��ϲ��Χ���ѧ����Լ�ж����ˣ�
���𰸡���1��0.36����2����ͼ����������3��420��
�������������������1�����ȸ���Χ������14�ˣ�Ƶ����0.28���ݴ˼��������������Ȼ������18�����������������a��ֵ��
��2����50����0.20���b��ֵ�����ɽ��
��4����������1500����ϲ��Χ���ѧ��Ƶ�ʼ�����⣮
�����������1��14��0.28=50���ˣ���
a=18��50=0.36��
��2��b=50��0.20=10����ͼ��

��3��1500��0.28=420���ˣ���
����ȫУ����ѧ��1500�������Ƹ�У��ϲ��Χ���ѧ����Լ��420�ˣ�


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. x2x2��x6B. x4��x��x2
C. ����x��y������x+yD. 3x2x��6x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɫ�о��꼶�μ��п�����Լ��38900�ˣ�����38900�ÿ�ѧ��������ʾΪ��������
A.3.89��102
B.389��102
C.3.89��104
D.3.89��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ֱ���ܵ���ͬ��㡢ͬ�յ㡢ͬ���������ܲ�500�ף��ȵ��յ����ԭ����Ϣ����֪���ȳ���2�룮���ܲ������У��ס������˵ľ���y���ף����ҳ�����ʱ��t���룩֮��Ĺ�ϵ��ͼ��ʾ���������½��ۣ���a=8����b=92����c=123��������ȷ���ǣ������� 
A.�٢ڢ�
B.�٢�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С����������һ�����⣺��ͼ1���ڡ�ABC�У�DE��BC�ֱ�AB��D����AC��E����֪CD��BE��CD=3��BE=5����BC+DE��ֵ��
С�����֣�����E��EF��DC����BC�ӳ����ڵ�F�������BEF�����������ͼ����ܹ�ʹ
����õ��������ͼ2����
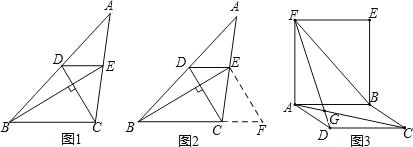
��1����ش�BC+DE��ֵΪ������
��2���ο�С��˼������ķ�����������⣺
��ͼ3����֪ABCD�;���ABEF��AC��DF���ڵ�G��AC=BF=DF�����AGF�Ķ�����
��ͼ4����֪��AB��CD����E�㣬����AD��BC��AD=3![]() ��BC=1���ҡ�B���D��Ϊ��ǣ���A���C��Ϊ���ǣ����AED= �ȣ���CD=
��BC=1���ҡ�B���D��Ϊ��ǣ���A���C��Ϊ���ǣ����AED= �ȣ���CD=![]() ����AB�ij���
����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD��AB��EF��AB������ֱ�ΪD��F����1=��2��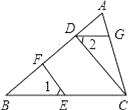
��1�����ж�DG��BC��λ�ù�ϵ����˵�����ɣ�
��2������A=70�㣬��B=40�㣬���AGD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���x2+2kx+k2��6��0
��1��֤������������������ȵ�ʵ������
��2�����������һ����Ϊ2������2k2+8k+2018��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���нְڷ���������ס��ҡ����������͵��辰�������辰��15��컨��24��ƻ���25���ϻ�������ɣ������辰��10��컨��12��ƻ�������ɣ������辰��10��컨��18��ƻ���25���ϻ�������ɣ���Щ�辰һ������2900��컨��3750���ϻ�����ƻ�һ�����˶��ٶ䣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com