
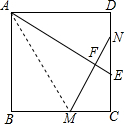
 如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为2$\sqrt{5}$-4.
如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为2$\sqrt{5}$-4. 分析 根据正方形的性质得到AD=CD=2,∠D=∠B=90°,根据勾股定理得到AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{5}$,根据折叠的性质得到AF=AB=2,∠AFN=∠B=90°,根据相似三角形的性质得到NE=5-2$\sqrt{5}$,于是得到结论.
解答  解:∵在正方形ABCD中,AB=2,
解:∵在正方形ABCD中,AB=2,
∴AD=CD=2,∠D=∠B=90°,
∵E是CD中点,
∴DE=1,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{5}$,
∵将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,
∴AF=AB=2,∠AFN=∠B=90°,
∴EF=$\sqrt{5}$-2,∠NFE=90°,
∴∠D=∠NFE,
∵∠AED=∠NEF,
∴△ADE∽△NFE,
∴$\frac{AE}{NE}=\frac{DE}{EF}$,即$\frac{\sqrt{5}}{NE}$=$\frac{1}{\sqrt{5}-2}$,
∴NE=5-2$\sqrt{5}$,
∴DN=DE-NE=2$\sqrt{5}$-4,
故答案为:2$\sqrt{5}$-4.
点评 本题考查了翻折变换-折叠问题,相似三角形的判定和性质,正方形的性质,勾股定理,正确的理解题意是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$.
《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com