
【题目】一副三角板如图1所置,其中AC边与等腰Rt△EBD斜边上的中线EC共线,以C点为旋转中心,顺时针转动△ACB,B、A两点分别于G、F两点对应,CG交BE边于点M,CF交DE边于N,已知旋转角为α,BC=2.
(问题发现)(1)如图2所示,若旋转角α(0°<α<30°)时,猜想CM与CN的数量关系,并写出你的推断过程;
(类比探究)(2)如图3所示,若旋转角α=75°时,(1)中的结论是否还成立? ,此时连接MN,请直接写出MN的长度为 ;
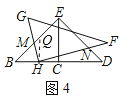
(拓展延伸)(3)在图3的基础上将△GCF向左平移至△GHF的位置,若DH=kBH,猜想线段HN与HM的数量关系.

【答案】(1)CM=CN,证明详见解析;(2)成立,![]() ;(3)HN=kHM.
;(3)HN=kHM.
【解析】
(1)根据等腰三角形的性质得到EC⊥CD,EC=CD=BC,证明△BCM≌△ECN,根据全等三角形的性质证明结论;
(2)作CP⊥BE于点P,根据等腰直角三角形的性质求出PC,根据余弦的定义求出CM,根据等腰直角三角形的性质计算,得到答案;
(3)作HQ∥EC,证明△MHQ∽△NHD,根据相似三角形的性质解答即可.
解:(1)CM=CN,
理由如下:在Rt△BED中,EB=ED,BC=CD,
∴EC⊥CD,EC=CD=BC,∠BEC=∠DEC=∠B=∠D=45°,
∵∠BCM+∠ECM=90°,∠ECN+∠ECM=90°,
∴∠BCM=∠ECN,
在△BCM和△ECN中,
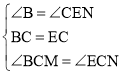
∴△BCM≌△ECN(ASA)
∴CM=CN;
(2)(1)中的结论成立, ![]() ,
,
理由如下:作CP⊥BE于点P,(1)中的结论成立,证明过程同(1)相同,
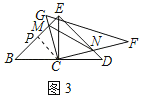
在Rt△BCP中,∠B=45°,
∴PC=BCsinB=![]() ,
,
∵∠BCM=75°,∠BCP=45°,
∴∠PCM=30°,
∴CM=![]() =
=![]() ,
,
在等腰直角三角形MCN中,MN=![]() PC=
PC=![]() ,
,
故答案为:成立;![]() ;
;
(3)HN=kHM,
理由如下:过点H作HQ∥EC交BE于点Q,
则△BHQ为等腰直角三角形,
∴BH=HQ,
∵DH=kBH,
∴DH=kQH,
∵∠MHQ+∠QHF=90°,∠NHD+∠QHF=90°,
∴∠MHQ=∠NHD,又∠MQH=∠NDH,
∴△MHQ∽△NHD,
∴![]() =
=![]() =k,即HN=kHM.
=k,即HN=kHM.


科目:初中数学 来源: 题型:
【题目】结合书香成都全民阅读活动,金堂在全县中小学推广普及中华经典诵读,让孩子掌握国学经典作品“读、诵、吟”等基本方法,培养中华经典诵读活动的爱好者、传播者,营造浓郁的文化氛围.2018年9月某初中学校开展了国学金典诵读活动,林老师对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
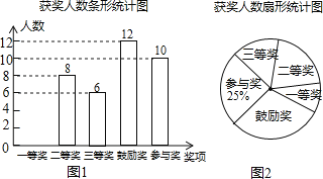
(1)请将条形统计图补全;
(2)获得一等奖的同学中有1名来自七年级,有2名来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加县级国学经典诵读大赛,请用列表或画树状图的方法求所选出的两人中既有七年级又有八年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()
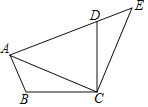
A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
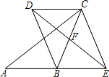
![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的业余文化生活,某校教务处准备在大课间期间开设兴趣小组,预设科目为“舞蹈”“音乐”“电竞”“动漫”为了准确配备教室与师资,负责人制作了“你最喜欢的科目”的调查问卷,在校园随机调查后制作了两幅不完整的统计图,请你根据信息解答下面问题:

(1)本次调查中,参与问卷调查的人数为 ;
(2)扇形统计图中的m、n的值为 、 ,补全条形统计图;
(3)若该校有学生2000人,请你估计报名“电竞”的学生的人数为 ;
(4)最先报名“动漫”课程的三名学生中有两名男生一名女生,若随机抽取两名学生参与教室网线布设,求两名学生恰为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年“五一”假期,某教学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示,斜坡AB的长为200![]() 米,斜坡BC的长为200
米,斜坡BC的长为200![]() 米,坡度是1:1,已知A点海拔121米,C点海拔721米
米,坡度是1:1,已知A点海拔121米,C点海拔721米
(1)求B点的海拔;
(2)求斜坡AB的坡度;
(3)为了方便上下山,若在A到C之间架设一条钢缆,求钢缆AC的长度.
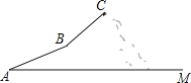
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?
(精确到米,参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin67°≈
,sin67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
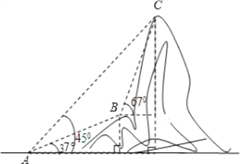
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球沿着足够长的光滑斜面向上滚动,它的速度与时间满足一次函数关系,其部分数据如下表:

(1) 求小球的速度v与时间t的关系.
(2)小球在运动过程中,离出发点的距离S与v的关系满足![]() ,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
(3)求时间为多少时小球离出发点最远,最远距离为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com