
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

【答案】(1) 45°;(2) P(2,-3);(3)![]() .
.
【解析】
(1)由抛物线解析式可得三角形各点坐标,判断三角形形状,即可得到其内角;
(2)过点D作DH⊥x轴于点H,由不规则图象面积分割求和的方法求得面积,得到点E坐标,再求得直线ED解析式,联立抛物线方程即可得到点P坐标;
(3)先分别表示出点F和点P坐标,再利用已知条件用其坐标表示线段PF的长度,再根据二次函数性质求得其最大值即可.
解:(1)A(-1,0),B(3,0),C(0,-3),D(1,-4).∵OC=OB=3,∴△OBC为等腰直角三角形,∴∠OBC=45°.
(2)过点D作DH⊥x轴于点H,此时S四边形OCDB=S梯形OCDH+S△HBD,∵OH=1,OC=3,HD=4,HB=2,∴S梯形OCDH=·(OC+HD)·OH=,S△HBD=·HD·HB=4,∴S四边形OCDB=![]() .∴S△OCE=S四边形OCDB=
.∴S△OCE=S四边形OCDB=![]() =·OC·OE,∴OE=5,∴E(5,0).∴lDE:y=x-5.∵DE交抛物线于P,设P(x,y),∴x2-2x-3=x-5,解得 x=2 或x=1(D点,舍去),∴xP=2,代入lDE:y=x-5,∴P(2,-3).
=·OC·OE,∴OE=5,∴E(5,0).∴lDE:y=x-5.∵DE交抛物线于P,设P(x,y),∴x2-2x-3=x-5,解得 x=2 或x=1(D点,舍去),∴xP=2,代入lDE:y=x-5,∴P(2,-3).
(3)如图,lBC:y=x-3.∵F在BC上,∴yF=xF-3.∵P在抛物线上,∴yP=x-2xP-3,∴PF=yF-yP=xF-3-(x-2xP-3).∵xP=xF,∴PF=-x+3xP=-(xP-)2+ (1<xP<3),∴当xP=时,线段PF长度最大,最大值为.


科目:初中数学 来源: 题型:
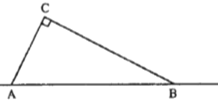
【题目】如图,![]() 为一条公路,现有一处
为一条公路,现有一处![]() 需要爆破,爆破点
需要爆破,爆破点![]() 周围
周围![]() 范围内有危险,已知点
范围内有危险,已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() ,与停靠站
,与停靠站![]() 的距离为
的距离为![]() ,且
,且![]() .
.
(1)通过计算说明公路![]() 段是否存在危险;
段是否存在危险;
(2)直接写出公路![]() 存在危险的路段长度.
存在危险的路段长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运城的桃子今年获得了大丰收,现A,B两个水果合作社要向甲,乙两个市场运送桃子,已知A可调出110吨,B可调出90吨,甲地需要80吨,乙地需要120吨,两地到甲乙市场的路程和费用如图:
路程(km) | ||
A地 | B地 | |
甲农贸市场 | 15 | 20 |
乙农贸市场 | 22 | 25 |
(1)设A地运往甲市场的桃子![]() 吨(0≤
吨(0≤![]() ≤80),则A地运往乙市场的桃子有__________吨,B地运往甲市场的桃子有___________吨,B地运往乙市场的桃子有__________吨.
≤80),则A地运往乙市场的桃子有__________吨,B地运往甲市场的桃子有___________吨,B地运往乙市场的桃子有__________吨.
(2)若每吨桃子每千米需要运费12元,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(3)当A地给甲农贸市场运多少吨桃子时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用6万元购进一批新款衬衫,上架后很快销售一空.商场马上又购进第二批这种衬衫,数量是第一次的1.6倍,但每件进价涨了2元,结果共用去12.8万元.
(1)问该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件都是按78元销售,当库存还有156件时打八折销售,问全部销售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
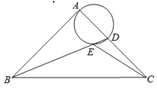
A. 3 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:(1)三角形的一条中线把三角形分成面积相等的两部分;(2)有两边及其中一边的对角对应相等的两三角形全等;(3)点![]() 关于原点的对称点坐标为
关于原点的对称点坐标为![]() ;(4)若
;(4)若![]() ,则
,则![]() ;其中真命题的有 ( )
;其中真命题的有 ( )
A. (1)、(2)B. (1)、(3)C. (2)、(3)D. (3)、(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将 n 个边长都为 1cm 的正方形按如图所示的方法摆放,点 A1,A2,…,An 分别是正方形对角线的交点,则 6 个正方形重叠形成的重叠部分的面积和为( )cm2.
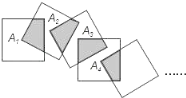
A.![]() B.1C.
B.1C.![]() D.(
D.(![]() )5
)5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com