
【题目】阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
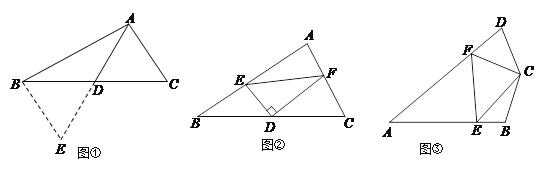
(1)如图①,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】(1) ![]() (2)证明见解析(3)BE+DF=EF
(2)证明见解析(3)BE+DF=EF
【解析】试题分析:(1)延长AD至E,使DE=AD,连接BE.由SAS证明△BDE≌△CDA,得出BE=AC=6,在△ABE中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
(2)延长FD至点G,使DG=DF,连接BG,EG.同(1)得△BDG≌△CDF,得出BG=CF,由线段垂直平分线的性质得出EF=EG,在△BEG中,由三角形的三边关系得出BE+BG>EG即可得出结论;
(3)延长AB至点G,使BG=DF,连接CG.证出∠CBG=∠D,由SAS证明△CBG≌△CDF,得出CG=CF,∠BCG=∠DCF,证出∠ECG=70°=∠ECF,再由SAS证明△ECG≌△ECF,得出EG=EF,即可得出结论.
解:(1)延长AD至E,使DE=AD,连接BE,如图①所示:
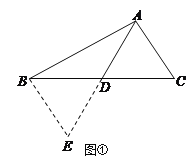
∵AD是BC边上的中线,∴BD=CD,在△BDE和△CDA中,∵BD=CD,∠BDE=∠CDA,DE=AD,∴△BDE≌△CDA(SAS),∴BE=AC=6,在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,∴12﹣8<AE<12+8,即4<AE<20,∴2<AD<10;
(2)证明:延长FD至点G,使DG=DF,连接BG,EG.
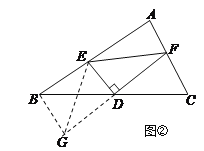
∵点D是BC的中点,∴DB=DC.
在△BDG和△CDF中,
∵DG=DF,∠BDG=∠CDF,DB=DC,∴△BDG≌△CDF(SAS),∴BG=CF.
∵ED⊥FD,即ED⊥FG.
又∵FD=GD,∴EF=EG.
在△BEG中,∵BE+BG>EG, ∴BE+CF>EF.
(3)解:BE+DF=EF.证明如下:
如图,延长AB至点G,使BG=DF,连接CG.
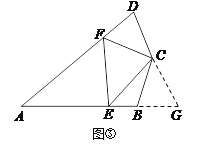
∵∠ABC+∠D=180°,∠ABC+∠CBG=180°,∴∠CBG=∠D.
在△CBG和△CDF中,
∵BG=DF,∠CBG=∠CDF,CB=CD,∴△CBG≌△CDF(SAS), ∴CG=CF,∠BCG=∠DCF,.
∵∠BCD=140°,∠ECF=70°,∴∠DCF+∠BCE=70°,∴∠BCE+∠BCG=70°,∴∠ECG=∠ECF=70°.
在△ECG和△ECF中,
∵CE=CE,∠ECG=∠ECF,CG=C,∴△ECG≌△ECF(SAS),∴EG=EF.
∵BE+BG=EG,∴BE+DF=EF.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=108°,则∠C的度数为( )

A. 40° B. 41° C. 32° D. 36°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com