
【题目】如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)
(参考数据:sin43° =0.6820, cos43° =0.7314, tan43° =0.9325

 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3),

(1)①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出△ABC绕原点O逆时针旋转90°得到的△A2B2C2,写出点C2的坐标;
(2)若△ABC上任意一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则点Q的坐标为________.(用含m,n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边长![]() 与另一边长
与另一边长![]() 之间的函数图像如图.
之间的函数图像如图.

(1)该绿化带的面积是多少?写出![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)完成下表,并回答问题:如果该绿化带的长![]() 不得超过
不得超过![]() ,那么
,那么![]() 应控制在什么范围?
应控制在什么范围?
| 10 | 20 | 30 | 40 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
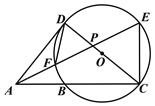
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=16,点P从点A出发,沿AB方向以每秒2个长度单位的速度向点B运动:同时点Q从点C出发,沿CA方向以每秒3个长度单位的速度向点A运动,其中一点到达终点,则另一点也随之停止运动,当△ABC与以A、P、Q为顶点的三角形相似时,运动时间为______秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
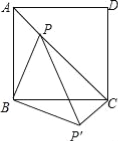
【题目】如图,P为正方形ABCD内一点,且BP=2,PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′,则AP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线CD与以线段OB为直径的半⊙A相切于点C,连接OC、BC,作OD⊥CD,垂足为D,OB=10,

(1)求证:∠OCD=∠OBC;
(2)如图②,作CE⊥OB于点E,若CE=AE,求线段OD的长;
(3)如图③,在(2)的条件下,以O点为原点建立平面直角坐标系求△DOB外接圆的圆心坐标.
以下是优优和乐乐两位同学对第(3)小题的讨论
优优:这题很简单嘛,我只要求出这个三角形任意两条边的中垂线解析式,然后求交点坐标就行了.乐乐:我还有其他的好方法.
如果你是乐乐,你会怎么做?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD,E、F分别为BC、CD边上一点.
(1)若∠EAF=45°,求证:EF=BE+DF;
(2)若该正方形ABCD的边长为1,如果△CEF的周长为2.求∠EAF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com