
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA、PB、AB、OP,已知PB是⊙O的切线.
(1)求证:∠PBA=∠C;
(2)若OP∥BC,且OP=9,⊙O的半径为3![]() ,求BC的长.
,求BC的长.
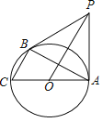
【答案】(1)证明见解析;(2)BC=4.
【解析】
(1)连接OB,根据切线的性质和圆周角定理求出∠PBO=∠ABC=90°,即可求出答案;
(2)求出△ABC∽△PBO,得出比例式,代入求出即可.
(1)连接OB,
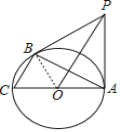
∵PB是⊙O的切线,∴PB⊥OB,∴∠PBA+∠OBA=90°,
∵AC是⊙O的直径,∴∠ABC=90°,∠C+∠BAC=90°,
∵OA=OB,∴∠OBA=∠BAO,∴∠PBA=∠C;
(2)∵⊙O的半径是3![]() ,
,
∴OB=3![]() ,AC=6
,AC=6![]() ,∵OP∥BC,∴∠BOP=∠OBC,
,∵OP∥BC,∴∠BOP=∠OBC,
∵OB=OC,∴∠OBC=∠C,∴∠BOP=∠C,∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴BC=4.
,∴BC=4.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
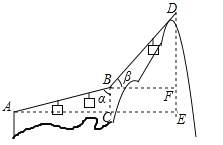
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
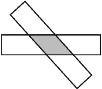
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是( )

A. 10B. 12C. 20D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为6 cm,母线OE(OF)长为9cm.在母线OF上的点A处有一块爆米花残渣,且FA = 3cm.在母线OE上的点B处有一只蚂蚁,且EB = 1cm.这只蚂蚁从点B处沿圆锥表面爬行到A点,则爬行的最短距离为 cm.
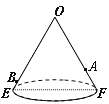
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积是 ,边长是 .
(2)把10个小正方形组成的图形纸(如图2),剪开并拼成正方形.
①请在4×4方格图内画出这个正方形.
②以小正方形的边长为单位长度画一条数轴,并在数轴上画出表示-![]() 的点.
的点.
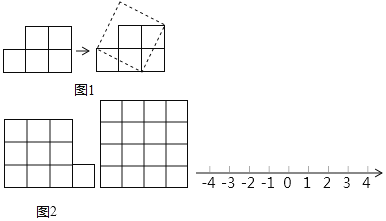
(3)这种研究和解决问题的方式,主要体现了 的数学思想方法.
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
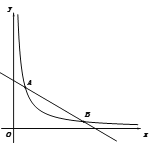
【题目】如图,已知一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和点B(m,1)
(x>0)的图象交于点A(2,6)和点B(m,1)
(1)求一次函数和反比例函数的解析式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com