
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 首先根据题意画出表格,然后由表格求得所有等可能的结果与数字x、y满足y=-x+5的情况,再利用概率公式求解即可求得答案.
解答 解:列表得:
| 1 | 2 | 3 | 4 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) |
点评 此题考查的是用列表法或树状图法求概率与不等式的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
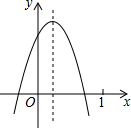 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
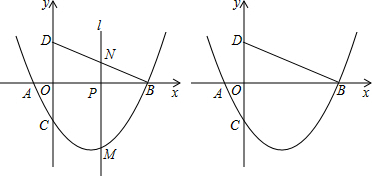
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
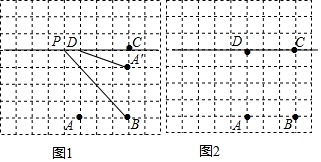
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )| A. | 22 | B. | 36 | C. | 46 | D. | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
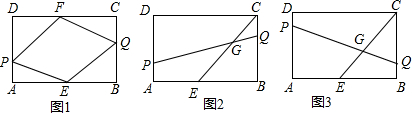
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com