
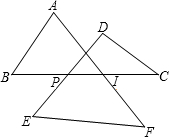
 如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )
如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )| A. | 安佶从家到新华书店的平均速度是10千米/分钟 | |
| B. | 安佶买书花了15分钟 | |
| C. | 安佶吃早餐花了20分钟 | |
| D. | 从早餐店到安佶家的1.5千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△A′B′C′是△ABC经过平移得到的,A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图所示,△A′B′C′是△ABC经过平移得到的,A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
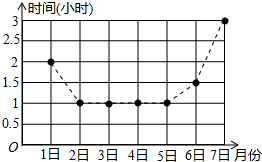 如图是小浩同学8月1日〜7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是3小时,这七天平均每天的自主学习时间是1.5小时.
如图是小浩同学8月1日〜7日毎天的自主学习时间统计图,则小浩同学一天中自主学习时间最长是3小时,这七天平均每天的自主学习时间是1.5小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com