
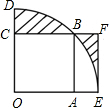
 如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、$\widehat{DE}$、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为2$\sqrt{2}$-2cm2.
如图:扇形DOE的圆心角为直角,它的半径为2cm,正方形OABC内接于扇形,点A、B、C分别在OE、$\widehat{DE}$、OD上,过E作EF⊥OE交CB的延长线于F,则图中阴影部分的面积为2$\sqrt{2}$-2cm2. 分析 根据S阴=S扇形OBD-S△OBC+S梯形OBFE-S扇形OBE计算即可.
解答 解:连接OB.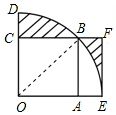
由题意可知OD=OE=2,OC=BC=OA=AB=$\sqrt{2}$,
S阴=S扇形OBD-S△OBC+S梯形OBFE-S扇形OBE=$\frac{2+(2-\sqrt{2})}{2}•\sqrt{2}$-$\frac{1}{2}$$•\sqrt{2}$•$\sqrt{2}$=2$\sqrt{2}$-2.
故答案为2$\sqrt{2}$-2.
点评 本题考查矩形的性质、扇形的面积公式、正方形的性质等知识,解题的关键是记住扇形的面积公式,学会利用分割法求阴影部分面积,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
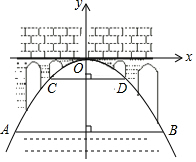 如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)
如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
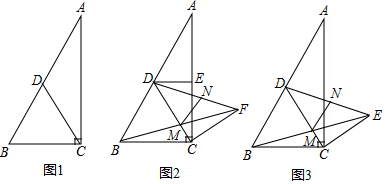
 如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.
如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com