
分析 (1)分子分母直接约分化简即可.
(2)分子分母因式分解后约分即可.
(3)先计算括号后计算除法即可.
(4)根据先乘除后加减,有乘方的先计算乘方法则进行计算即可.
解答 解:(1)原式=ab.
(2)原式=$\frac{(x+1)(x-1)}{x(x-1)}$=$\frac{x+1}{x}$.
(3)原式=$\frac{1-x+2}{x-2}$•$\frac{(x+2)(x-2)}{3-x}$=x+2.
(4)原式=$\frac{{a}^{2}}{{b}^{2}}$•$\frac{5b}{4{a}^{2}}$+$\frac{a}{2b}$=$\frac{5}{4b}$+$\frac{a}{2b}$═$\frac{5+2a}{4b}$.
点评 本题考查分式的混合运算,熟练掌握分式的混合运算法则是解题的关键,记住因式分解的公式和方法,灵活掌握运算顺序,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
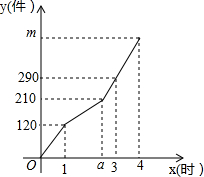 某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
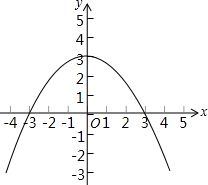 如图,在平面直角坐标系中画出了函数y=ax2+c的图象.
如图,在平面直角坐标系中画出了函数y=ax2+c的图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
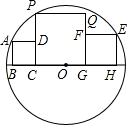 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com