
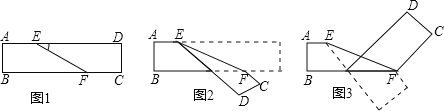
【题目】如图1是长方形纸袋,将纸袋沿EF折叠成图2,再沿BF折叠成图3,若∠DEF=α,用α表示图3中∠CFE的大小为 _________ .
【答案】180°-3α.
【解析】
试题分析:先根据进行的性质得AD∥BC,则∠BFE=∠DEF=α,根据折叠的性质,把如图1中的方形纸袋沿EF折叠成图2,则∠MEF=α,把图2沿BF折叠成图3,则∠MFH=∠CFM,根据平行线的性质由FH∥MG得到∠MFH=180°-∠FMG,再利用三角形外角性质得∠FMG=∠MFE+∠MEF=2α,则∠MFH=180°-2α,所以∠CFM=180°-2α,然后利用∠CFE=∠CFM-∠EFM求解.
试题解析:
在图1中,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠BFE=∠DEF=α,
∵如图1中的方形纸袋沿EF折叠成图2,
∴∠MEF=α,
∵图2再沿BF折叠成图3,
∴在图3中,∠MFH=∠CFM,
∵FH∥MG,
∴∠MFH=180°-∠FMG,
∵∠FMG=∠MFE+∠MEF=α+α=2α,
∴∠MFH=180°-2α,
∴∠CFM=180°-2α,
∴∠CFE=∠CFM-∠EFM=180°-2α-α=180°-3α.


科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.﹣1的平方根是﹣1
B.4的平方根是2
C.如果一个数有平方根,那么这个数的平方根一定有两个
D.任何一个非负数的立方根都是非负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2= ![]() .过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E.
.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E. 
(1)求证: ![]() ;
;
(2)若PQ=2,试求∠E度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
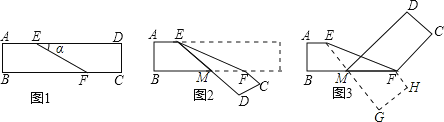
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
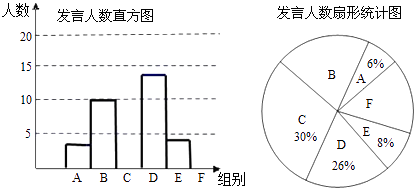
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=90°,抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M.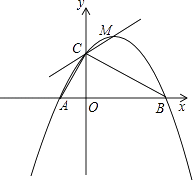
(1)求抛物线y=ax2+bx+c的解析式;
(2)试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
(3)在抛物线上是否存在点N,使得S△BCN=4?如果存在,那么这样的点有几个?如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择. 方案一:每千克种子价格为4元,无论购买多少均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次性购买超过3千克的,则超过3千克的部分的种子价格打7折.
(1)请分别求出方案一和方案二中购买的种子数量x(千克)和付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com