
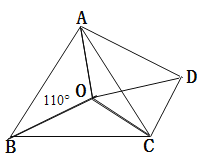
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,以OC为一边作等边△OCD,连接AD.
(1)求证:△BOC≌△ADC;
(2)当OA=OD时,求a的值
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.
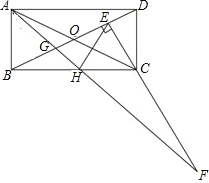
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2 a -7,B=a2- 4a+3,C= a2 +6a-28,其中![]() .
.
(1)求证:B-A>0,并指出A与B的大小关系;
(2)阅读对B因式分解的方法:
解:B=a2- 4a+3=a2- 4a+4-1=(a-2)2-1=(a-2+1)(a-2-1)=(a-1)(a-3).
请完成下面的两个问题:
①仿照上述方法分解因式:x2- 4x-96;
②指出A与C哪个大?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是△ABC边BC上一点,AD=BD,且AD平分∠BAC.(1)若∠B=50°,求∠ADC的度数;(2)若∠C=30°,求∠ADC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2017年12月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:7×9﹣1×15= ,18×20﹣12×26= ,不难发现,结果都是 .

(1)请将上面三个空补充完整;
(2)我们发现选择其他类似的部分规律也相同,请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在![]() 处,BC为折痕。
处,BC为折痕。
(1)图①中,若∠1=30°,求∠![]() 的度数;
的度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠![]() 的度数;
的度数;
(3)如果在图②中改变∠1的大小,则![]() 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠![]() 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com