
分析 (1)①提公因式后再利用平方差公式分解因式;
②利用了两次完全平方公式进行因式分解;
③提公因式$\frac{1}{2}$ab后,再利用完全平方公式进行因式分解;
(2)先利用乘法分配律去括号,约分后,再去括号,代入求值即可.
解答 解:(1)①2x3-18x=2x(x2-9)=2x(x+3)(x-3);
②(x2+2x)2+2(x2+2x)+1,
=(x2+2x+1)2,
=(x+1)4;
③$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3,
=$\frac{1}{2}$ab(a2+2ab+b2),
=$\frac{1}{2}$ab(a+b)2,
当a+b=2,ab=2时,原式=$\frac{1}{2}$×2×22=4;
(2)($\frac{3x}{x-1}$-$\frac{2x}{x+1}$)•$\frac{{x}^{2}-1}{x}$,
=$\frac{3x}{x-1}$•$\frac{(x+1)(x-1)}{x}$-$\frac{2x}{x+1}$$•\frac{(x+1)(x-1)}{x}$,
=3(x+1)-2(x-1),
=x+5,
当x=$\sqrt{5}$-5时,原式=$\sqrt{5}$-5+5=$\sqrt{5}$.
③$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3
点评 本题既考查出因式分解及应用,又考查了分式的化简求值,计算量不大,但要细心完成;做好本题的关键是熟练掌握完全平方公式和平方差公式.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
 阅读理解下面内容,并解决问题:
阅读理解下面内容,并解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 图形个数( n ) | (1) | (2) | (3) |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=12x | B. | y=18x | C. | y=$\frac{2}{3}$x | D. | y=$\frac{3}{2}x$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
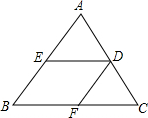 如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)
如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com