
如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒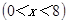 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.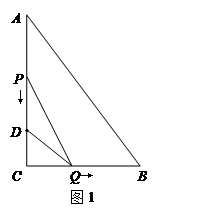
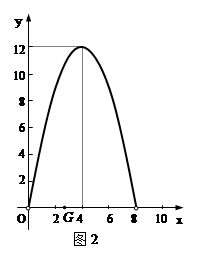
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6),过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
(1)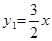 .图象如图所示:
.图象如图所示: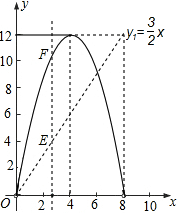
(2)点P的速度每秒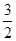 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①表示△PCQ与△DCQ的面积差(或△PDQ面积);②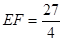
解析试题分析:(1)已知了CD=3,根据Q点的速度可以用时间x表示出CQ的长,可根据三角形的面积计算公式得出y1,x的函数关系式;
(2)可先求出y2的函数式,然后根据其顶点坐标来确定k的取值.已知了P点走完AC用时8s,因此AC=8k,而AP=kx,CQ=x,那么可根据三角形的面积公式列出关于y2,x的函数关系式,进而可根据顶点坐标求出k的值;
(3)EF其实就是y2-y1,也就是三角形PCQ和CDQ的面积差即三角形PDQ的面积.得出EF的函数关系式后,根据自变量的取值以及函数的性质即可求出EF的最大值.
(1)∵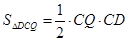 ,CD=3,CQ=x,
,CD=3,CQ=x,
∴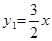 .图象如图所示:
.图象如图所示:
(2) ,CP=8k-xk,CQ=x,
,CP=8k-xk,CQ=x,
∴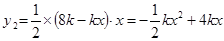 .
.
∵抛物线顶点坐标是(4,12),
∴ .解得
.解得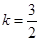
则点P的速度每秒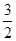 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①观察图象,知线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积)
②由(2)得 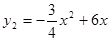 .
.
∵EF=y2-y1,
∴EF=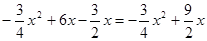 ,
,
∵二次项系数小于0,
∴在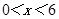 范围,当
范围,当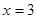 时,
时,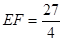 最大.
最大.
考点:二次函数的综合题
点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,主要考查学生对二次函数的熟练掌握情况.


科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com