
 ��ͼ��?ABCD�У�AD=3cm��AB=5cm��BD��AD����P�ӵ�A��������AD���������˶���ͬʱ��Q�ӵ�B��������BA���������˶��������˶����ٶ�Ϊ1cm/s�����˶���ʱ��Ϊx��s������CPQ�����Ϊy��cm2��������Q�˶�����Aʱ��P��Q��ֹͣ�˶���
��ͼ��?ABCD�У�AD=3cm��AB=5cm��BD��AD����P�ӵ�A��������AD���������˶���ͬʱ��Q�ӵ�B��������BA���������˶��������˶����ٶ�Ϊ1cm/s�����˶���ʱ��Ϊx��s������CPQ�����Ϊy��cm2��������Q�˶�����Aʱ��P��Q��ֹͣ�˶������� ��1����������֤����CDP�ס�CBQ���������������ε������г�����ʽ�����x��ֵ��
��2�����ݹ��ɶ������AB�����������ε������ʽ���DE������ƽ���ߵ��������PH�����ͼ����x��ʾ��y��
��3�����ݶ��κ����������������y����Сֵ�͵�y=5.5ʱ���Ա���x��ȷ��x��ȡֵ��Χ��
��� �⣺��1����AP=BQ=x��AB=5��AD=3��
��PD=3-x��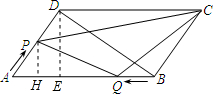
���ı���ABCD��ƽ���ı��Σ�
���CDP=��CBQ��CD=AB=5��BC=AD=3��
�ߡ�PCD=��QCB��
���CDP�ס�CBQ��
��$\frac{CD}{CB}=\frac{PD}{BQ}$����$\frac{5}{3}=\frac{3-x}{x}$��
���x=$\frac{9}{8}$��
��2����DE��AB��E��PH��AB��H��
��AD=3cm��AB=5cm��BD��AD��
��BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=4��
��DE=$\frac{AD��BD}{AB}$=$\frac{12}{5}$��
��PH��DE��
��$\frac{PH}{DE}$=$\frac{AP}{AD}$����$\frac{x}{3}$=$\frac{PH}{\frac{12}{5}}$��
��ã�PH=$\frac{4}{5}$x��
���CPQ�����Ϊy=Sƽ���ı���ABCD-S��APQ-S��CBQ-S��PDC
=12$-\frac{1}{2}��$��5-x����$\frac{4}{5}$x-$\frac{1}{2}$��$\frac{12}{5}$x-$\frac{1}{2}��$5����$\frac{12}{5}$-$\frac{4}{5}$x��
=$\frac{2}{5}$x2-$\frac{6}{5}$x+6��
��3��y=$\frac{2}{5}$x2-$\frac{6}{5}$x+6=$\frac{2}{5}$��x-$\frac{3}{2}$��2+5.1��
��y����СֵΪ5.1��
��y=5.5ʱ��$\frac{2}{5}$x2-$\frac{6}{5}$x+6=5.5��
��ã�x1=$\frac{1}{2}$��x2=$\frac{5}{2}$��
��4��y��5.5ʱ��x��ȡֵ��ΧΪ$\frac{1}{2}$��x��$\frac{5}{2}$��
���� ���⿼����Ǿ��ε����ʡ����������ε��ж������ʡ����κ����������Լ����κ�������ֵ��ȷ�����������������ε��ж����������ʶ����������䷽��������κ�������Сֵ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
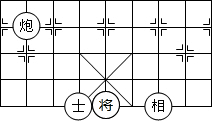 �й��������й�������ǧ�������ʷ�����������У�Ȥζ��ǿ���仯�ḻϸ�壬�����������ֶ��������й��Ļ�����ͼ�����
�й��������й�������ǧ�������ʷ�����������У�Ȥζ��ǿ���仯�ḻϸ�壬�����������ֶ��������й��Ļ�����ͼ����� ����λ�õ�����Ϊ��-1��-1����
����λ�õ�����Ϊ��-1��-1���� ����λ�õ�����Ϊ��2��-1������ô��
����λ�õ�����Ϊ��2��-1������ô�� ����λ�õ�����Ϊ��-3��2����
����λ�õ�����Ϊ��-3��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
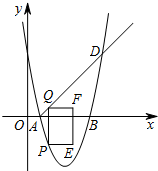 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
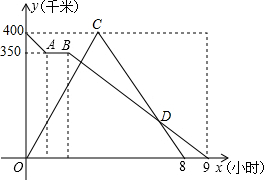 �ס�����������·����400ǧ�ף��졢������ͬʱ�����س������������ҵ�ʻ��أ���;���ͣ��1Сʱ������ԭ·ԭ��ʻ��أ��쳵�Ӽ�ʻ���ҵأ��ڵ����ҵغ�������ԭ·ԭ�ٷ��ص��أ���������ʻ�Ĺ����У�������ص�·��y��ǧ�ף���������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ������ͼ�������м��⣺
�ס�����������·����400ǧ�ף��졢������ͬʱ�����س������������ҵ�ʻ��أ���;���ͣ��1Сʱ������ԭ·ԭ��ʻ��أ��쳵�Ӽ�ʻ���ҵأ��ڵ����ҵغ�������ԭ·ԭ�ٷ��ص��أ���������ʻ�Ĺ����У�������ص�·��y��ǧ�ף���������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ������ͼ�������м��⣺�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com