
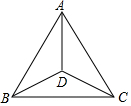
 ��֪����D��������ABC����ƽ���ڵ�����һ�㣬���������жϣ�����BD=DC��AD��BC����AB=AC��������BAD=��CAD��BD=DC����AB=AC��������D���߶�BC�ϣ���$\frac{BD}{DC}=\frac{AB}{AC}$ʱ����BAD=��CAD��������D���߶�BC�ϣ���AB=AC=3ʱ��AD2+BD•DCΪ��ֵ��������ȷ���ǣ�������
��֪����D��������ABC����ƽ���ڵ�����һ�㣬���������жϣ�����BD=DC��AD��BC����AB=AC��������BAD=��CAD��BD=DC����AB=AC��������D���߶�BC�ϣ���$\frac{BD}{DC}=\frac{AB}{AC}$ʱ����BAD=��CAD��������D���߶�BC�ϣ���AB=AC=3ʱ��AD2+BD•DCΪ��ֵ��������ȷ���ǣ�������| A�� | �٢� | B�� | �ڢ� | C�� | �٢ڢ� | D�� | �٢ۢ� |
���� ���ɵ������������ߺ�һ�ã���BDE=��CDE��֤����ABD�ա�ACD���ɵ�AB=AC��
�ڸ���������ͼ����ͼ2������AB��AC��һ����ȣ�
����ͼ3���������ߣ�����ƽ���ߣ�����ƽ���߷��߶γɱ��������ã�$\frac{BD}{CD}=\frac{AB}{AF}$���ɵ�AF=AC���ɵȱ߶ԵȽǵá�F=��ACF����ƽ���ߵ����ʵó����ۣ���BAD=��CAD��
����ͼ4��������AE�����ݹ��ɶ����ã�AB2=AE2+BE2��AD2=AE2+DE2���ɵ������������ߺ�һ�ã�BE=CE����ǰ��ʽ�������οɵý��ۣ�
���  �⣺����ͼ1�����ӳ�AD��BC��E����AE��BC��
�⣺����ͼ1�����ӳ�AD��BC��E����AE��BC��
��BD=DC��
���BDE=��CDE��
���ADB=��ADC��
�ڡ�ABD�͡�ACD�У�
��$\left\{\begin{array}{l}{AD=AD}\\{��ADB=��ADC}\\{BD=CD}\\{\;}\end{array}\right.$��
���ABD�ա�ACD��SAS����
��AB=AC��
���Ԣ���ȷ��
����ͼ2������BAD=��CAD��BD=DC����AB��AC��
���Ԣڲ���ȷ��
�۹�C��CF��AD����BA���ӳ����ڵ�F��
��$\frac{BD}{CD}=\frac{AB}{AF}$��
��$\frac{BD}{CD}=\frac{AB}{AC}$��
��AF=AC��
���F=��ACF��
��AD��CF��
���BAD=��F����CAD=��ACF��
���BAD=��CAD��
���Ԣ���ȷ��
����ͼ4����AE��BC��E����AB2=AE2+BE2��AD2=AE2+DE2��
��AB=AC��
��BE=CE��
��AB2-AD2=��AE2+BE2��-��AE2+DE2��=BE2-DE2=��BE+DE����BE-DE��=BD•DC��
��AD2+BD•DC=AB2=32=9��
���Ե�AB=AC=3ʱ��AD2+BD•DCΪ��ֵ�� ���Ԣ���ȷ��
���Ԣ���ȷ��
���ԣ�������ȷ���ǣ��٢ۢܣ�
��ѡD��
���� ���⿼����������ȫ�ȵ����ʺ��ж���ƽ���߷��߶γɱ������������������ε����ʺ��ɶ�������������Ѷȣ������ߵ������ǹؼ�������4�����ù��ɶ�����ʽ���οɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 27 | C�� | 81 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У�AD��BC����C=132�㣬����A��AE��BC������DE����DEƽ�֡�ADC�����AED�Ķ�����
��ͼ���ı���ABCD�У�AD��BC����C=132�㣬����A��AE��BC������DE����DEƽ�֡�ADC�����AED�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a|��|b|������$\sqrt{��a+b��^{2}}$-|a-b|��
��֪ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a|��|b|������$\sqrt{��a+b��^{2}}$-|a-b|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ�����ǰ尴��ͼ��ʽ�ڷţ��õ���ABD�͡�BCD�����С�ADB=��BCD=90�㣬��A=60�㣬��CBD=45�㣬EΪAB���е㣬����E��EF��CD�ڵ�F����AD=4cm����EF�ij�Ϊ��$\sqrt{2}$+$\sqrt{6}$��cm��
һ�����ǰ尴��ͼ��ʽ�ڷţ��õ���ABD�͡�BCD�����С�ADB=��BCD=90�㣬��A=60�㣬��CBD=45�㣬EΪAB���е㣬����E��EF��CD�ڵ�F����AD=4cm����EF�ij�Ϊ��$\sqrt{2}$+$\sqrt{6}$��cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����д�����ǣ�������
��ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����д�����ǣ�������| A�� | ��AB=BCʱ���������� | B�� | ��AC��BDʱ���������� | ||
| C�� | ��AC=BDʱ�����Ǿ��� | D�� | ����ABC=90��ʱ������������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{4}$ | B�� | -4 | C�� | 4 | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com