
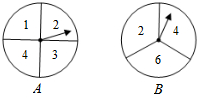
 ��ͼ����A��B����ת�̣�����ת��A���ֳ�4�ȷݣ�ת��B���ֳ�3�ȷݣ�����ÿһ���ڱ������֣��ּס�������ͬʱ��ת������һ��ת�̣�ת��ֹͣ��ָ��ָ�ڱ߽�����ʱ��Ϊ��Ч����ת��������Aת��ָ��ָ������ּ�Ϊx��Bת��ָ��ָ������ּ�Ϊy���Ӷ�ȷ����P������ΪP��x��y����
��ͼ����A��B����ת�̣�����ת��A���ֳ�4�ȷݣ�ת��B���ֳ�3�ȷݣ�����ÿһ���ڱ������֣��ּס�������ͬʱ��ת������һ��ת�̣�ת��ֹͣ��ָ��ָ�ڱ߽�����ʱ��Ϊ��Ч����ת��������Aת��ָ��ָ������ּ�Ϊx��Bת��ָ��ָ������ּ�Ϊy���Ӷ�ȷ����P������ΪP��x��y�������� ��1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����
��2�����ȸ�����״ͼ���s��6������������ø��ʹ�ʽ������ü�ʤ���һ�ʤ�ĸ��ʣ��Ƚϴ�С������֪��˭������
��3��ֻҪ������ͬ���ɣ����s=x+y����s��6ʱ����ʤ�������һ�ʤ��
��� �⣺��1������״ͼ�ã�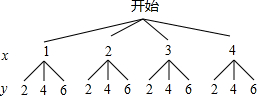
����12�ֵȿ��ܵĽ����
��2����s��6��4�������
��P����ʤ��=$\frac{4}{12}$=$\frac{1}{3}$��P���һ�ʤ��=$\frac{8}{12}$=$\frac{2}{3}$��
�������Ϸ����ƽ������������
��3����s=x+y����s��6ʱ����ʤ�������һ�ʤ��
���� ���⿼�������Ϸ��ƽ�Ե��жϣ��ж���Ϸ��ƽ�Ծ�Ҫ����ÿ���¼��ĸ��ʣ�������Ⱦ�ƽ������Ͳ���ƽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
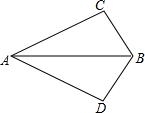 ��ͼ����ABC=��ABD��AC=AD������AAS������Ҫʹ��ABC�ա�ABD�����벹���һ�������ǡ�CAB=��DAB��
��ͼ����ABC=��ABD��AC=AD������AAS������Ҫʹ��ABC�ա�ABD�����벹���һ�������ǡ�CAB=��DAB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �μ��ʱ��С����С����С�յ�λ����ͼ��С����С��˵������ҵ�λ���ã�0��0����ʾ��С����λ���ã�-2��-1����ʾ����ôС�����λ�ÿ��Ա�ʾ�ɣ�������
�μ��ʱ��С����С����С�յ�λ����ͼ��С����С��˵������ҵ�λ���ã�0��0����ʾ��С����λ���ã�-2��-1����ʾ����ôС�����λ�ÿ��Ա�ʾ�ɣ�������| A�� | ��5��4�� | B�� | ��4��3�� | C�� | ��2��2�� | D�� | ��3��4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com