
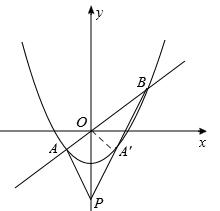
 交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法:
交于A,B两点,且A点在y轴左侧,P点的坐标为(0,﹣4),连接PA,PB.有以下说法: 时,BP2=BO•BA;
时,BP2=BO•BA; .
.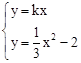 得:
得: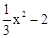 =kx,即x2﹣3kx﹣6=0,∴m+n=3k,mn=﹣6。
=kx,即x2﹣3kx﹣6=0,∴m+n=3k,mn=﹣6。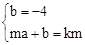 ,解得
,解得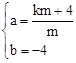 。∴直线PA的解析式为
。∴直线PA的解析式为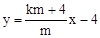 。
。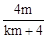 ,∴直线PA与x轴的交点坐标为(
,∴直线PA与x轴的交点坐标为(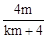 ,0)。
,0)。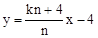 ,直线PB与x轴交点坐标为(
,直线PB与x轴交点坐标为(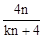 ,0)。
,0)。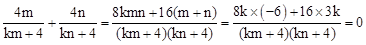 ,
,
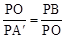 。
。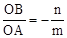 ,∴
,∴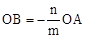 。
。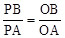 。∴
。∴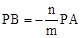 。
。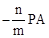 ﹣(
﹣( )]
)]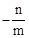 (PA+AO)(PA﹣OA)=
(PA+AO)(PA﹣OA)=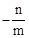 (PA2﹣AO2)。
(PA2﹣AO2)。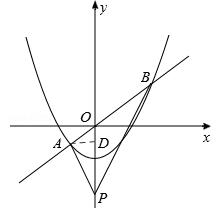
 (m+n)。
(m+n)。 (m+n)•m+16=
(m+n)•m+16=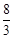 m2+
m2+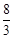 mn+16=
mn+16=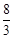 m2+
m2+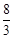 ×(﹣6)+16=
×(﹣6)+16=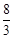 m2。
m2。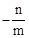 (PA2﹣AO2)=
(PA2﹣AO2)=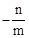 •
•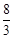 m2=﹣
m2=﹣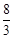 mn=﹣
mn=﹣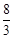 ×(﹣6)=16。
×(﹣6)=16。 时,联立方程组:
时,联立方程组: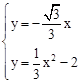 ,得A(
,得A(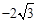 ,2),B(
,2),B( ,﹣1),
,﹣1),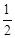 OP•(﹣m)+
OP•(﹣m)+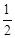 OP•n=
OP•n=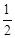 OP•(n﹣m)=2(n﹣m)
OP•(n﹣m)=2(n﹣m)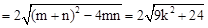 ,
, 。故说法④正确。
。故说法④正确。

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
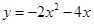 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象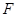 .
.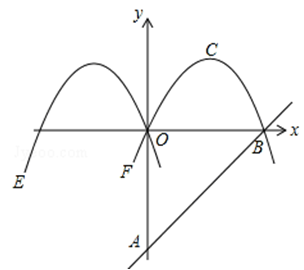
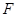 所表示的抛物线的解析式:
所表示的抛物线的解析式: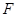 和
和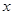 轴相交于点
轴相交于点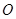 、点
、点 (点
(点 位于点
位于点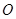 的右侧),顶点为点
的右侧),顶点为点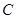 ,点
,点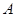 位于
位于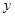 轴负半轴上,且到
轴负半轴上,且到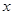 轴的距离等于点
轴的距离等于点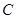 到
到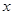 轴的距离的2倍,求
轴的距离的2倍,求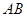 所在直线的解析式.
所在直线的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
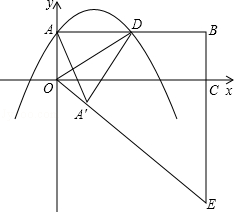
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
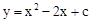 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为﹣4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
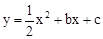 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)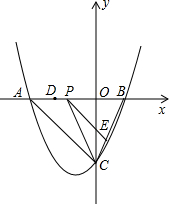
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
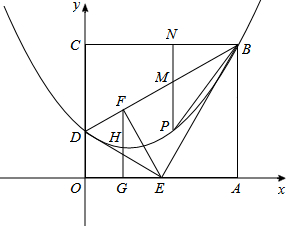
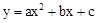 经过B,H, D三点,求抛物线解析式;
经过B,H, D三点,求抛物线解析式;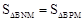 如果存在,求出点P的坐标;如果不存在,请说明理由.
如果存在,求出点P的坐标;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
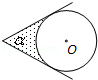
A.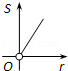 | B. | C.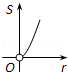 | D.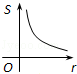 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com