
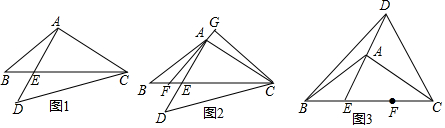
分析 (1)如图1中,作DF⊥BC于F,AN⊥BC于N,连接BD.首先证明点B、D、C在以A为圆心的圆上,推出△BDF是等腰直角三角形,再证明tan∠ABC=tan∠ACB=tan∠FDE=tan∠EAN=$\frac{1}{2}$,设EN=a,则AN=2a,CN=BN=4a,推出BF=DF=2a,EF=a,EC=5a,再根据AC=2$\sqrt{5}$a=2$\sqrt{2}$,求出a即可解决问题.
(2)如图2中,连接DF,延长AF交BD于M.首先证明△BFD是等腰直角三角形,再证明△AMD≌△CGA,推出AG=DM=BM=FM,CG=AM,由△BFD是等腰直角三角形,FM⊥BD,推出∠BFM=∠AFN=45°,推出$\sqrt{2}$BF=$\sqrt{2}$AN=AF,由此即可证明.
(3)如图3中,作AM⊥BC于M,连接DF.FA的延长线交BD于N.首先证明BD=$\sqrt{2}$BF,由sin∠ABC=$\frac{1}{2}$,推出∠ABC=∠ACB=∠EAM=30°,设EM=m则AE=2m,EC=4m,AM=FM=$\sqrt{3}$m,CF=CM=FM=3m-$\sqrt{3}$m,FG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$,由此即可解决问题.
解答 (1)解:如图1中,作DF⊥BC于F,AN⊥BC于N,连接BD.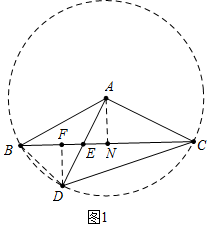
∵AB=AD=AC,
∴点B、D、C在以A为圆心的圆上,
∵DA⊥AC,
∴∠DAC=90°,
∴∠DBC=$\frac{1}{2}$∠DAC=45°,
∵∠DFB=90°,
∴△BDF是等腰直角三角形,
∴DF=BF,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACE+∠AEC=90°,∠FDE+∠FED=90°,∠FED=∠AED,
∴∠FDE=∠ACB=∠ABC,
∵∠EAN+∠AEC=90°,∠ACB+∠AEC=90°,
∴∠EAN=∠ACB,
∴tan∠ABC=tan∠ACB=tan∠FDE=tan∠EAN=$\frac{1}{2}$,设EN=a,则AN=2a,CN=BN=4a,
∴BE=3a,
∵BF=DF=2EF,
∴BF=DF=2a,EF=a,CE=5a,
在Rt△ADC中,∵CD=4,
∴AD=AC=2$\sqrt{2}$,
又∵AC=$\sqrt{A{N}^{2}+N{C}^{2}}$=$\sqrt{(2a)^{2}+(4a)^{2}}$=2$\sqrt{5}$a,
∴2$\sqrt{5}$a=2$\sqrt{2}$,
∴a=$\frac{\sqrt{10}}{5}$,
∴EC=5a=$\sqrt{10}$.
(2)证明:如图2中,连接DF,延长AF交BD于M.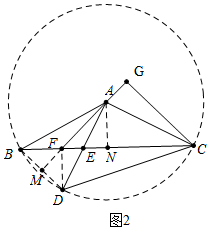
∵AF平分∠BAD,
∴∠FAB=∠FAD,
在△FAB和△FAD中,
$\left\{\begin{array}{l}{AB=AD}\\{∠FAB=∠FAD}\\{AF=AF}\end{array}\right.$,
∴△FAB≌△FAD,
∴BF=DF,
∴∠DBF=∠FDB=45°,
∴DF⊥BC,
∵AB=AD,MA平分∠BAD,
∴BM=DM,AM⊥BD,
∵∠DAM+∠CAG=90°,∠CAG+∠ACG=90°,
∴∠MAD=∠ACG,∵AD=AC,∠AMD=∠G=90°,
∴△AMD≌△CGA,
∴AG=DM=BM=FM,CG=AM,
由(1)可知,BF=FN=AN,
∵△BFD是等腰直角三角形,FM⊥BD,
∴∠BFM=∠AFN=45°,
∴$\sqrt{2}$BF=$\sqrt{2}$AN=AF,
∴CG=AM=FM+AF=AG+$\sqrt{2}$BF.
∴$\sqrt{2}$BF+AG=CG.
(3)解:如图3中,作AM⊥BC于M,连接DF.FA的延长线交BD于N.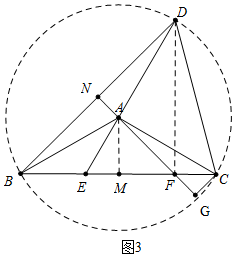
∵AB=AD,
∴AN⊥BD,BN=DN,
∴FB=FD,
∵∠CBD=$\frac{1}{2}$∠CAD=45°,
∴∠FBD=∠FDB=45°,
∴△BDF是等腰直角三角形,
∴BD=$\sqrt{2}$BF,
∵sin∠ABC=$\frac{1}{2}$,
∴∠ABC=∠ACB=∠EAM=30°,设EM=m则AE=2m,EC=4m,AM=FM=$\sqrt{3}$m,CF=CM=FM=3m-$\sqrt{3}$m,FG=$\frac{3m-\sqrt{3}m}{\sqrt{2}}$,
∴$\frac{BF•FG}{BD•AE}$=$\frac{BF}{\sqrt{2}BF}$•$\frac{\frac{3m-\sqrt{3}m}{\sqrt{2}}}{2m}$=$\frac{3-\sqrt{3}}{2}$.
点评 本题考查三角形综合题,圆的有关知识、全等三角形的判定和性质、等腰直角三角形的性质,30度的直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数,用方程的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
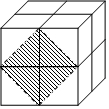 如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
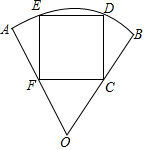 要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
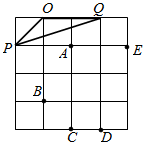 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.2 | -1 | +2 | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com