
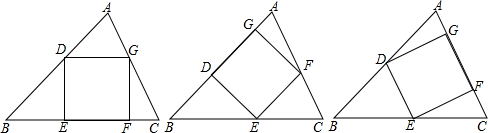
分析 设a、b、c分别△ABC中∠A、∠B、∠C的对边,每边上的高分别为ha,hb,hc,三个内接正方形的边长分别为xa、xb、xc,△ABC的面积为S,由三个内接正方形的面积都相等,于是得到xa=xb=xc,2S=aha=bhb=chc,通过△ADG∽△ABC,得到$\frac{{x}_{a}}{a}=\frac{{h}_{a}-{x}_{a}}{{h}_{a}}$,解得xa=$\frac{a{h}_{a}}{a+{h}_{a}}$=$\frac{2S}{a+{h}_{a}}$,同理xb=$\frac{2S}{b+{h}_{b}}$,于是得到a+ha=b+hb,得到a2b+2bS=b2a+2aS,分解因式得((b-a)(2S-ab)=0,证得b-a=0,a=b,同理a=c,于是得到结论.
解答 解:设a、b、c分别△ABC中∠A、∠B、∠C的对边,每边上的高分别为ha,hb,hc,三个内接正方形的边长分别为xa、xb、xc,△ABC的面积为S,
∵三个内接正方形的面积都相等,
∴xa=xb=xc,2S=aha=bhb=chc,
∵DG∥BC,
∴△ADG∽△ABC,
∴$\frac{{x}_{a}}{a}=\frac{{h}_{a}-{x}_{a}}{{h}_{a}}$,
解得:xa=$\frac{a{h}_{a}}{a+{h}_{a}}$=$\frac{2S}{a+{h}_{a}}$,
同理xb=$\frac{2S}{b+{h}_{b}}$,
∴a+ha=b+hb,
∴a$+\frac{2S}{a}$=b$+\frac{2S}{b}$,
∴a2b+2bS=b2a+2aS,
分解因式得((b-a)(2S-ab)=0,
∵2S-ab=aha-ab=a(ha-b)≠0(ha<b),
∴b-a=0,∴a=b,
同理a=c,
∴△ABC是等边三角形.
点评 本题考查了相似三角形的判定和性质,正方形的性质,等边三角形的判定,三角形的面积,熟记相似三角形的对应高的比等于相似比是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:单选题
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB于D,CD=1,则AB的长为( )

A. 2 B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
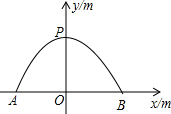 一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.
一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:填空题
已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为__________________

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com