
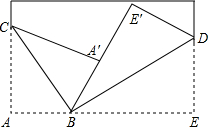
 如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.
如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.  走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
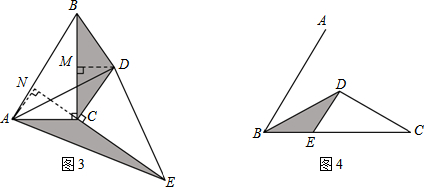
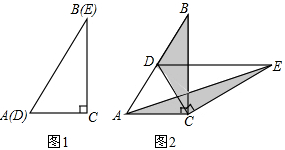 ,
,
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{3x}-20=\frac{10}{4x}$ | B. | $\frac{6}{3x}+20=\frac{10}{4x}$ | C. | $\frac{6}{3x}-\frac{1}{3}=\frac{10}{4x}$ | D. | $\frac{6}{3x}+\frac{1}{3}=\frac{10}{4x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)
如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com