
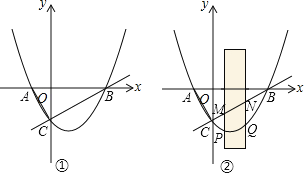
����Ŀ����ͼ�٣�ֱ��y��![]() ��x�ᡢy��ֱ��ڵ�B��C��������y��
��x�ᡢy��ֱ��ڵ�B��C��������y��![]() ��B��C���㣬����x�����һ������Ϊ��A������AC��
��B��C���㣬����x�����һ������Ϊ��A������AC��
��1���������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D�����A���غϣ���ʹ��S��DBC��S��ABC�������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3���п���Ϊ2�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��CB�ڵ�M�͵�N���ھ���ƽ�ƹ����У����Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ�����M�����꣮
���𰸡���1��![]() ����2�����ڣ���D��8��5�������ɼ���������3����M������Ϊ��2����2����2+2
����2�����ڣ���D��8��5�������ɼ���������3����M������Ϊ��2����2����2+2![]() ��
��![]() ��2����2��2
��2����2��2![]() ����
����![]() ��2��
��2��
��������
��1�����ô���ϵ�������ɽ�����⣮
��2����ͼ���У���AD��BC����������D����S��ABC=S��BCD�����ֱ��AD�Ľ���ʽ������������ȷ�����꼴�ɣ�
��3����M��m��![]() m-3������N��m+2��
m-3������N��m+2��![]() m-2�����ɵ�P��m��
m-2�����ɵ�P��m��![]() m2-m-3����Q[m+2��
m2-m-3����Q[m+2��![]() ��m+2��2-��m+2��-3]���Ƴ�PM=
��m+2��2-��m+2��-3]���Ƴ�PM=![]() m-3-��
m-3-��![]() m2-m-3����NQ=
m2-m-3����NQ=![]() m-2-[
m-2-[![]() ��m+2��2-��m+2��-3]����PM=QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ��ɴ˹������̼��ɽ�����⣮
��m+2��2-��m+2��-3]����PM=QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ��ɴ˹������̼��ɽ�����⣮
��1��������C��0����3����B��6��0������C��0����3����B��6��0������y��![]() +bx+c�õ�
+bx+c�õ�![]() �����
�����![]() ���������ߵĽ���ʽΪy��
���������ߵĽ���ʽΪy��![]() x2��x��3��
x2��x��3��
��2����ͼ���У���AD��BC����������D����S��ABC��S��BCD��
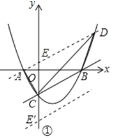
��ֱ��BC�Ľ���ʽΪy��![]() x��3��A����2��0������ֱ��AD�Ľ���ʽΪy��
x��3��A����2��0������ֱ��AD�Ľ���ʽΪy��![]() x+1����
x+1����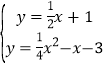 �����
�����![]() ��
��![]() ����D��8��5����
����D��8��5����
��ֱ��AD��y����E��0��1������E���ڵ�C�ĶԳƵ�E����0����7����
�����E��ƽ��BC��ֱ�ߵĽ���ʽΪy��![]() x��7����
x��7����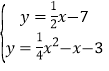 ���������⣬
���������⣬
����ֱ��BC���·����������������ĵ�D�������������ĵ�D��8��5����
��3����M��m��![]() m��3������N��m+2��
m��3������N��m+2��![]() m��2����
m��2����
��P��m��![]() m2��m��3����Q[m+2��
m2��m��3����Q[m+2��![]() ��m+2��2����m+2����3]��
��m+2��2����m+2����3]��
��PM��![]() m��3����
m��3����![]() m2��m��3����NQ��
m2��m��3����NQ��![]() m��2��[
m��2��[![]() ��m+2��2����m+2����3]��
��m+2��2����m+2����3]��
��PM��QNʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
��|![]() m��3����
m��3����![]() m2��m��3��|��|
m2��m��3��|��|![]() m��2��[
m��2��[![]() ��m+2��2����m+2����3]|��ã�m��2��2��2
��m+2��2����m+2����3]|��ã�m��2��2��2![]() ��
��
�����������ĵ�M������Ϊ��2����2����2+2![]() ��
��![]() ��2����2��2
��2����2��2![]() ����
����![]() ��2����
��2����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A������Ϊ��4��3������D�DZ�OC�ϵ�һ�㣬��E��ֱ��OB�ϣ�����DE��CE����DE+CE����СֵΪ��������
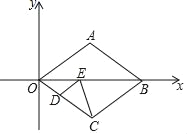
A. 5B. ![]() +1C. 2
+1C. 2![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ɳˮ����ʳ�������.��һ��ΰ��ë�ļѾ䣬���������������������.ij����ר������ij��Ʒ����հ�װ���������ʳ��Ʒ���ɱ�Ϊ30Ԫ/�У�ÿ������y(��)�����۵���x(Ԫ)֮�����һ�κ�����ϵ����ͼ��ʾ��
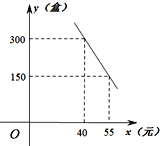
(1)��y��x֮��ĺ�����ϵʽ��
(2)����涨ÿ�������������ʳ��Ʒ��������������240�У������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
(3)������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3 600Ԫ����ȷ�������������ʳ��Ʒ���۵��۵ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
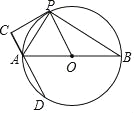
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����PC�С�O�ڵ�P����A��ֱ��AC��PC����O����һ��D������PA��PB��
(1)��֤��APƽ�֡�CAB��
(2)��P��ֱ��AB�Ϸ���Բ����һ���㣬��O�İ뾶Ϊ2����
�ٵ���AP�ij���_____ʱ����A��O��P��CΪ������ı����������Σ�
�ڵ�![]() �ij�����______ʱ����A��D��O��PΪ������ı��������Σ�
�ij�����______ʱ����A��D��O��PΪ������ı��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
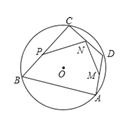
����Ŀ����ͼ��AB��BC�ǡ�O���ң���B��60������O�ڡ�B�ڣ���DΪ![]() �ϵĶ��㣬��M��N��P�ֱ���AD��DC��CB���е㣮����O�İ뾶Ϊ2����PN+MN�ij��ȵ����ֵ��________.
�ϵĶ��㣬��M��N��P�ֱ���AD��DC��CB���е㣮����O�İ뾶Ϊ2����PN+MN�ij��ȵ����ֵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() ����
����![]() ��ֱ������
��ֱ������![]() ����
����![]() ��һ�㣬
��һ�㣬 ![]() �����
�����![]() �����ߴ�ֱ������Ϊ��
�����ߴ�ֱ������Ϊ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ�![]() ����
����![]() ƽ����
ƽ����![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
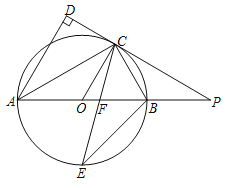
��1����֤�� ![]() ƽ����
ƽ����![]() ��
��
��2����֤��PC=PF��
��3����![]() ��AB=14�����߶�
��AB=14�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ĶԽ����ཻ�ڵ�
�ĶԽ����ཻ�ڵ�![]() ����
����![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���ܳ�Ϊ20����
���ܳ�Ϊ20����![]() ���ܳ�Ϊ�� ��
���ܳ�Ϊ�� ��
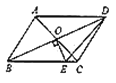
A. 7B. 8C. 9D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
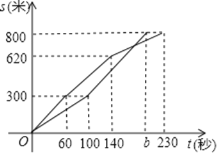
����Ŀ��ijУ�����꼶����Ů��800�ײ��ԣ��ס�������ͬѧͬʱ���ܣ���ͬѧ����a��/����ٶ������ܣ�һ��ʱ�������ٶȣ���![]() ��/����ٶ������ܣ�b�뵽���յ㣬��ͬѧ�ڵ�60��͵�140��ʱ�ֱ�������ٶȣ���ס�������ͬѧ����·��Ϊs���ף�����ͬѧ���õ�ʱ��Ϊt���룩��s��t֮��ĺ���ͼ����ͼ��ʾ��
��/����ٶ������ܣ�b�뵽���յ㣬��ͬѧ�ڵ�60��͵�140��ʱ�ֱ�������ٶȣ���ס�������ͬѧ����·��Ϊs���ף�����ͬѧ���õ�ʱ��Ϊt���룩��s��t֮��ĺ���ͼ����ͼ��ʾ��
��1����ͬѧ���ܵ��ٶ�Ϊ______��/�룻
��2����a��b��ֵ��
��3������ͬѧ���ȼ�ͬѧ60��ʱ��ֱ��д��t��ֵ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲOΪԲ�ģ��뾶Ϊ1�Ļ�����������A��B���㣬P�ǻ�![]() ��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������
��һ�㣨����A��B�غϣ�������OP�����POB=�������P��������
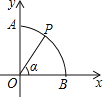
A. ��sin����sin���� B. ��cos����cos���� C. ��cos����sin���� D. ��sin����cos����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com